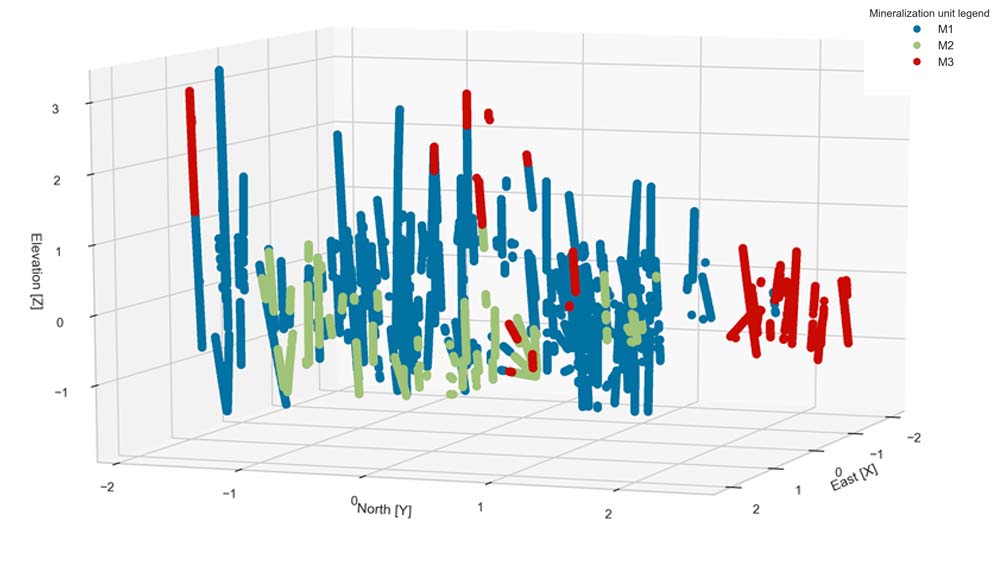
En el campo de la estimación de recursos minerales, es una práctica común identificar volúmenes espacialmente coherentes, estadísticamente similares y geológicamente distintos de otros volúmenes a su alrededor. Estos se denominan dominios de estimación en la literatura geoestadística (Rossi y Deutsch, 2013), y conllevan a una mejora en el rendimiento de las técnicas de estimación. Los aspectos geológicos del depósito suelen ser las pautas fundamentales para la definición de dominios de estimación. Atributos como la alteración, mineralización y aspectos litológicos deben ser considerados (Emery y Ortiz, 2004). Glacken & Snowden (2001) afirman que un dominio geológico representa un área o volumen dentro del cual las características de la mineralización son más similares que fuera del dominio. Rossi y Deutsch (2013), son más específicos y definen los dominios geológicos como el equivalente a zonas geoestadísticamente estacionarias.

Enfoque de agrupamiento automático:

En búsqueda de una alternativa en la definición de dominios de estimación, el cumplimiento de los principios de estimación geoestadística, la reducción en tiempo que se critica a la metodología tradicional y la disminución en la subjetividad, es que en esta reseña se presenta la implementación de una metodología basada en aprendizaje automático no supervisado, mediante el uso de un algoritmo de agrupamiento multivariable.

K-medias:

Uno de los algoritmos más populares y difundidos en el agrupamiento automático es k-medias, el cual corresponde a un método iterativo numérico, no supervisado, no determinista, que es simple y muy rápido, por lo que, en muchas aplicaciones prácticas, el método ha demostrado ser una forma muy efectiva que puede producir buenos resultados de agrupamiento (Na et al. 2010).

Oliver y Willingham (2016) utilizaron la agrupación de k-medias para identificar dominios geológicos en un depósito mineral de hierro con base en datos de análisis por laboratorio (Fe, SiO2, Al2O3, P, TiO2 y LOI).

Rajabinasab y Asghari (2019) utilizaron k-medias, para definir dominios geo-metalúrgicos en un depósito de hierro en el noreste de Irán, utilizando datos de análisis por laboratorio (Fe, FeO, S), susceptibilidad magnética y coordenadas espaciales X, Y, Z.

Moreira et al. (2020) utilizaron k-medias para definir dominios geológicos de estimación en un depósito de fosfato-titanio, utilizando principalmente datos de análisis por laboratorio (P2O5, TiO2 y CaO), tipo de roca y alteración.

K-prototipos como un enfoque de agrupamiento mixto:

Sin embargo, k-medias optimiza una función de costo definida en la medida de distancia euclidiana entre puntos de datos y medias. Minimizar la función de costo mediante el cálculo de medias limita su uso a datos numéricos (Huang, 1998). Esta limitación afecta a variables categóricas geológicas que controlan la ley mineral, no pudiendo aportar información en el agrupamiento. Dado este problema, se pueden transformar los datos categóricos a continuos, asumiendo un conocimiento absoluto de las asociaciones de las categorías de cada atributo geológico, lo cual es complejo. Lo segundo es realizar el proceso inverso, transformar las variables numéricas continuas de las leyes minerales, a discretas, asumiendo una pérdida importante de información, para luego emplear un algoritmo de agrupamiento para datos categóricos como k-modas (Huang, 1998). Bueno, como es de esperar, ambos arreglos no son buenos.

En la literatura, se han propuesto pocos métodos de agrupamiento para tratar con datos mixtos. Huang (1998) propuso el primer algoritmo que está basado en una combinatoria de k-medias y k-modas, al cual llamo k-prototipos, el que en este caso posibilita agrupar de manera conjunta leyes minerales y atributos geológicos. El algoritmo agrupa objetos con atributos numéricos y categóricos de una manera similar a k-medias.  La medida de similitud de objetos se deriva de atributos tanto numéricos como categóricos. Cuando se aplica a datos numéricos, el algoritmo es idéntico a k-medias.

Selección del número de dominios:

Al emplear algoritmos de aprendizaje no supervisado, los datos no están etiquetados, por lo que no se conoce la respuesta correcta a priori. En este caso los algoritmos de agrupamiento no jerárquicos requieren ser inicializados indicando el número de grupos como parámetro de entrada. Para la selección del número óptimo de grupos, se emplean dos heurísticas distintas, estas son el índice Calinski-Harabasz (Calinski y Harabasz 1974) y el coeficiente de Silueta (Rousseeuw 1987).

Como aplicarlo en un caso de estudio:

Los resultados experimentales mostrados por el método de k-prototipos han funcionado muy bien en conjuntos de datos pequeños y medianos, sin embargo, no logra tratar conjuntos de datos mixtos a gran escala (de millones de instancias), debido al alto costo computacional que requiere un total de n * k cálculos de distancia en cada iteración (Vattani, 2011).

En cuanto al flujo de trabajo general, es que se puede resumir de la siguiente manera: Imputación de datos faltantes en la muestra (sondajes), análisis exploratorio de datos (AED), selección de variables a emplear, estandarización de las variables; aplicación del algoritmo k-prototipos en 9 escenarios k, selección del k óptimo y finalmente validación de los dominios de estimación propuestos.

El AED tiene como propósito describir los atributos geológicos que controlan la ley mineral, y como esta se comporta a nivel estadístico y espacial en cada categoría de los atributos. De manera temprana se puede deducir si la ley mineral se agrupa en una única población o bien existen varias de forma independiente.

Un requerimiento en el agrupamiento automático es que cada una de las características tenga la misma influencia. Esto último lo resuelve la estandarización de datos. Se recomienda usar la Puntuación Z.

Posteriormente el algoritmo k-prototipos es ejecutado en 9 escenarios distintos para k, en un rango de 2 a 10. Esto con motivo de seleccionar el k optimo, que se condice con el numero de agrupamientos en el que la inercia dentro del grupo es mínima y al mismo tiempo se trata de grupos diferenciables entre ellos.

El primer método empleado para la selección del k optimo es el indice Calinski-Harabasz (Caliński and Harabasz, 1974), el cual relaciona las métricas internas de cohesión y separación. La cohesión se entiende como la cercanía que deben tener los miembros dentro de cada grupo y se puede evaluar con la suma de los cuadrados dentro de cada grupo.

Por otra parte, la separación habla de la disimilitud que debe existir entre grupos y se puede expresar en la suma de los cuadrados entre grupos.

Dado que el proceso de selección del k optimo puede ser arbitrario al solo confiar en un método, se utiliza un segundo método, llamado coeficiente de la silueta (Rousseeuw, 1987). Este método mide la distancia de separación entre los grupos, indica como de cerca está cada elemento de un grupo a elementos de los grupos vecinos. Esta medida de distancia se encuentra en el rango [-1, 1]. Un valor alto positivo significa un buen agrupamiento. Un valor cercano a 0 indica que el elemento está muy cerca o en la frontera de decisión entre dos grupos. Valores negativos indican que los elementos quizás estén asignadas al grupo erróneo. El método de la silueta calcula la media de los coeficientes de silueta de todas las observaciones para diferentes valores de k. El número óptimo “k” es aquel que maximiza la media de los coeficientes de silueta para un rango de valores de k.

Finalmente, los grupos resultantes, que son en definitiva los dominios de estimación, deben ser validados. Coombes (2016) propone un enfoque de revisión de varianza simple, basado en cuadrículas o similar, como requisito mínimo para la validación de dominios de estimación, sin embargo, recomendamos emplear de manera adicional el estimador del semivariograma (Matheron, 1963) para detectar dependencia espacial.  

Algunas figuras:

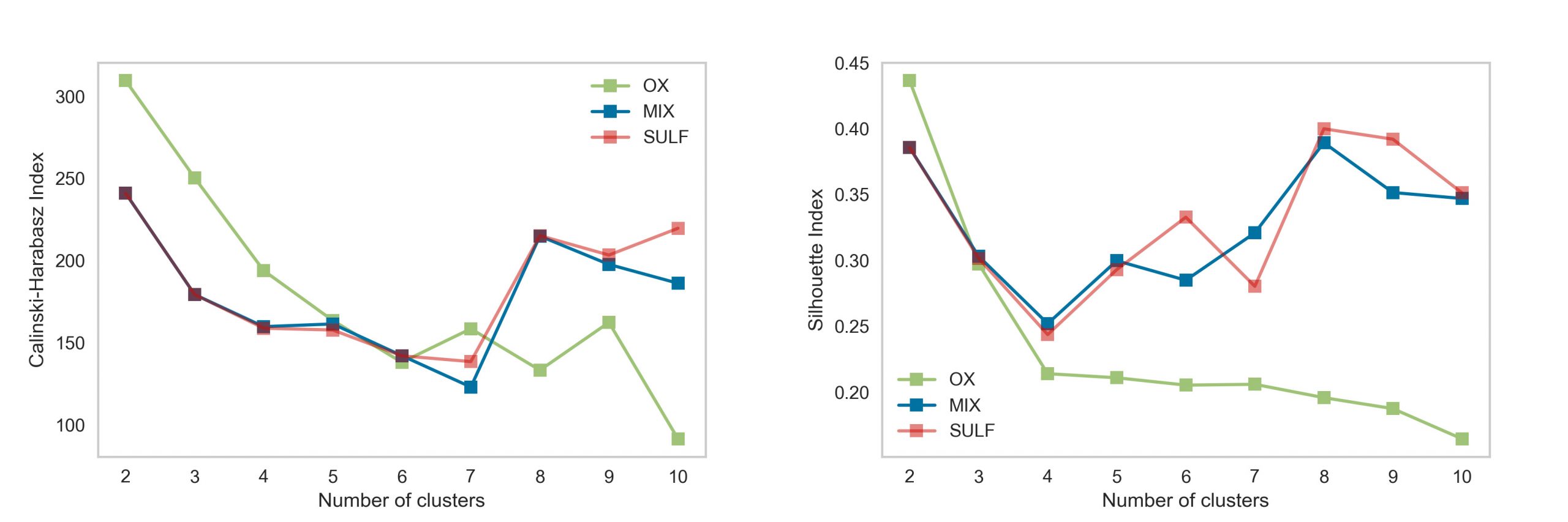
Resultados 9 escenarios de agrupamiento mixto por distintas zonas minerales utilizando leyes y variables geológicas categóricas. Método Caliński and Harabasz y la Silueta. 

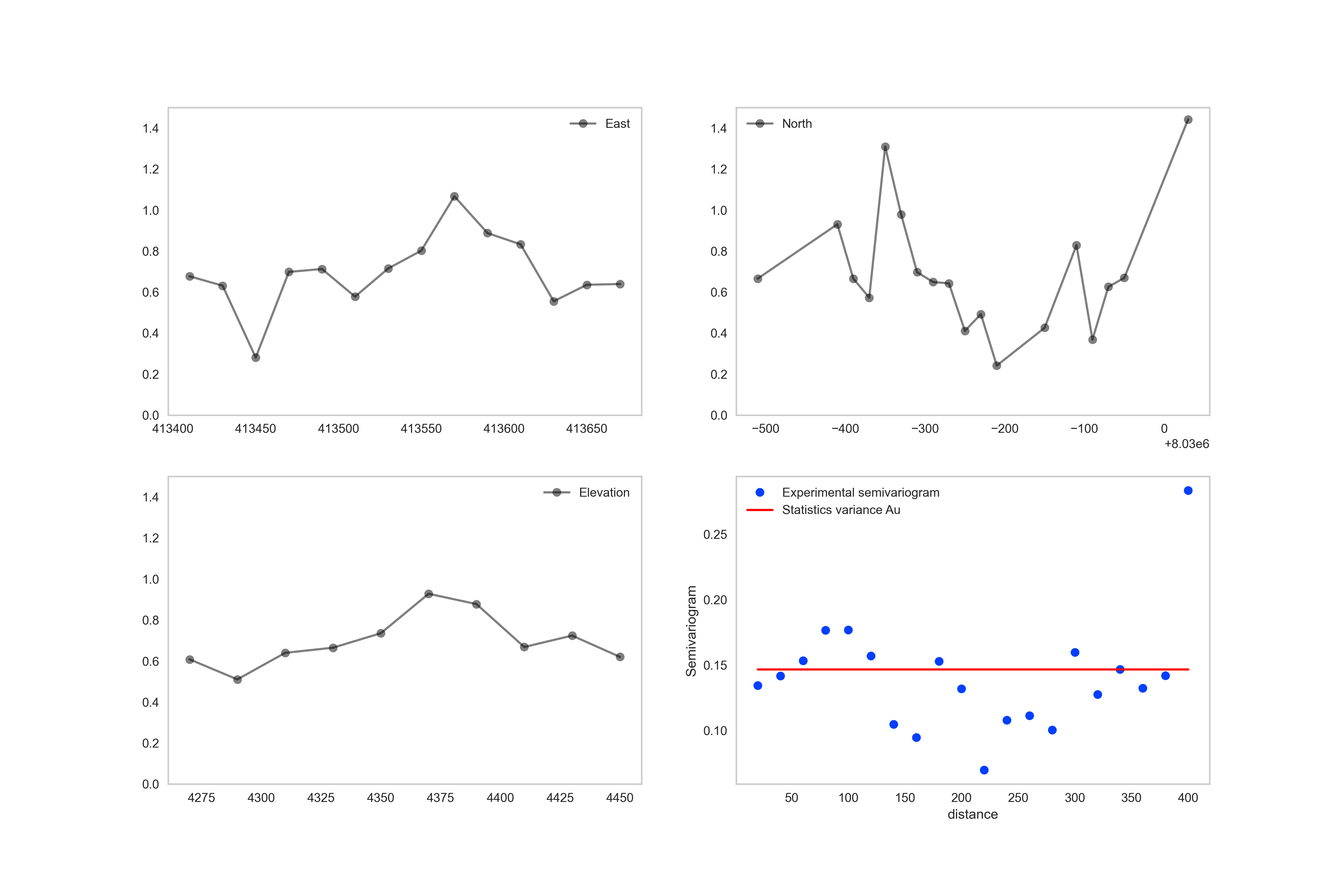
Resultados de uno de los dominios definidos mediante el enfoque de agrupamiento mixto; medias condicionales (X,Y,Z) y semivariograma omnidireccional.