
Introducción:
Dentro del machine learning se encuentra el aprendizaje no supervisado, denominado así debido a que infieren patrones de un conjunto de datos sin referencia a resultados conocidos o etiquetados. Esto nos indica que no hay un target u objetivo que predecir al momento de implementar los algoritmos, por lo que una de sus principales aplicaciones es la búsqueda de patrones por agrupamiento o clustering.
A continuación veremos cómo, con un algoritmo de clusterización, podemos lograr la compresión y segmentación de una imagen fotográfica de una roca en sección delgada, optimizando el costo computacional en el procesamiento. El algoritmo construye distintas particiones y las evalúa en función a criterios basados en distancia (métrica de similitud). Las siguientes imágenes corresponden a secciones delgadas donde se clusterizó en 2, 4, 9 y 15 colores; con el fin de mostrar las características de los distintos tipos de clusterizacion, y cuál sería la elección más apropiada de agrupamiento. Esto ultimo con motivo de encontrar la cantidad mínima de clusters con la que se pueda explicar la mayor parte de información.

Fig. 1: Sección delgada clusterisada en 2, 4, 9 y 15 colores (Caso I).
Terminología:
Clustering: El clustering (agrupamiento) consiste en dividir un conjunto de elementos heterogéneos en clústers o grupos homogéneos. El objetivo del agrupamiento es encontrar una división de los datos en la que se dé:
– Alta similaridad entre los elementos de un mismo clúster.
– Baja similaridad entre los elementos de distinto clústers.Función de Coste: En el contexto de agrupamiento, el coste cuantifica la heterogeneidad dentro cada grupo o cluster, y se obtiene como la suma de las distancias entre cada punto- y el centroide de su cluster.
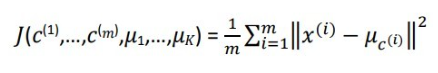
donde 𝜇𝑘 es el centroide del cluster 𝑘; 𝑐(𝑖) es el cluster al que ha sido asignado el elemento 𝑥(𝑖); y 𝜇𝑐(𝑖) es centroide del cluster al que ha sido asignado 𝑥(𝑖).
Desarrollo:
A continuación, se compararan los efectos de la clusterizacion en las imágenes de 2 secciones delgadas de rocas distintas. En primaria instancia, se procederá a calcular la función de coste para observar la variación de esta, en función del número de clusters (colores).
Caso I:
La gráfica de la función de coste para la primera sección delgada (Fig.1) muestra claramente que existe un punto a partir del cual la disminución del coste es significativamente más lenta. En concreto, hasta 9-10 colores, la disminución del coste es considerable. A partir de ese punto, la disminución es mucho más lenta. Esta circunstancia también se apreciará visualmente en las imágenes.
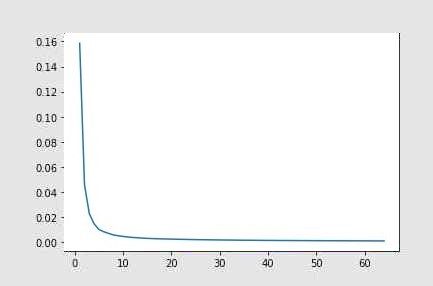
Fig. 2: Función de coste para la sección delgada del caso I.
En el caso I, se puede ver en las imágenes (Fig. 1) que la diferencia entre la imagen representada con 2 colores y la imagen representada con 4 colores es mucho más significativa que la diferencia entre la representada con 9 colores y la representada con 15.
Caso II:
La gráfica de la función de coste para la segunda sección delgada (Fig.3), muestra claramente que existe un punto a partir del cual la disminución del coste es significativamente más lenta. En concreto, hasta 4-5 colores, la disminución del coste es considerable. A partir de ese punto, la disminución es mucho más lenta. Esta circunstancia también se puede apreciar visualmente en las imágenes.
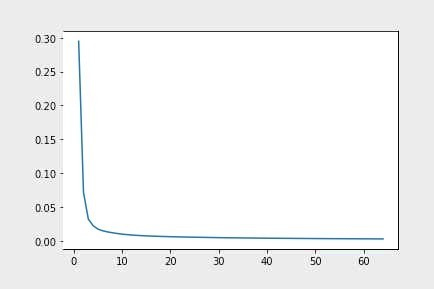
Fig.3 Función de coste para la sección delgada del caso II.
Para el caso II se puede ver (Fig. 4) que solo hay una diferencia significativa entre la imagen representada con 2 colores y la imagen representada por 4 colores; las imágenes representadas con 4 colores, 9 colores y 15 colores no muestran una diferencia significativa. Esto se debe a la función de coste.
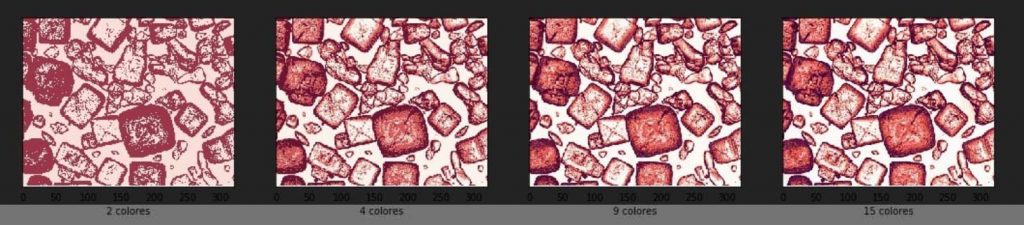
Fig.4 Sección delgada clusterisada en 2, 4, 9 y 15 colores (Caso II).
Análisis de los Resultados y Conclusiones:
De los ejemplos descritos anteriormente, se entiende que al estudiar la variación de la función de coste, se puede definir un número de agrupamientos (clusters=k), que explique la información en su gran mayoría y a la vez reduzca el numero de datos, optimizando tiempo y recursos. Se ha observado que a partir de un número determinado de clusters (cantidad de colores con la que se esta agrupando), la función de coste decrece muy lentamente.
Además es importante mencionar que ese número determinado de clusterizacion en donde empieza el decrecimiento lento, variará dependiendo de la imagen (input). Mientras más clases de datos posea (colores distintos) el valor k (número de cluster a partir del cual el descenso es más lento) será mayor, lo cual se observa a continuación en la gráfica (Fig. 5) de la función de coste y su respectiva imagen, donde a partir de k = 15 (15 colores) el descenso empieza a hacerse lento, diferente a los casos anteriores donde esto ocurría cuando k =4 y k = 9.
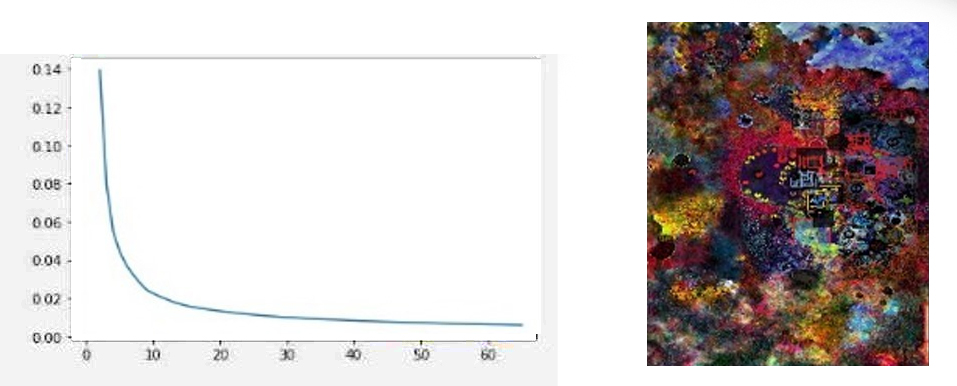
Fig.5: Variación función de coste en imagen con mayor cantidad de colores
Se observa que el valor de la función de coste empieza a descender más lento desde k =15. Esto se debe a la mayor cantidad de colores que posee la imagen.
Finalmente, es importante destacar que el uso de este algoritmo permite reducir el costo computacional para el procesamiento de imágenes, ya que se puede reducir la cantidad de dimensiones o características (en los ejemplos la cantidad de colores usados) manteniendo la mayor representatividad posible.
Aldo D. Carlos Villazana (Geologo), Linkedin


Debe estar conectado para enviar un comentario.