
INTRODUCCIÓN:
La necesidad de transparencia en la divulgación de recursos minerales, ha traído como consecuencia el desarrollo de códigos de categorización, que vienen a regular la industria minera, transmitiendo el riesgo de la inversión en los proyectos.
Los códigos de categorización de recursos en su mayoría, están destinados a proporcionar protección al inversor y, por lo general, son aplicados por las comisiones de valores u otras agencias gubernamentales apropiadas en cada país.
En el mundo se usan diferentes estándares de categorización de recursos. Si bien, todos poseen similares intensiones y forma, cada uno tiene sus propias particularidades.
Los estándares más reconocidos son:
Código JORC (Joint Ore Reserves Committee), Australasia, 1989. Modificado posteriormente el 1999.
Las guías CIM utilizadas en “National Instrument 43-101” Estándares de divulgación para Proyectos de Minerales (NI 43-101), Canadá, 1997.
El código SAMREC, Sudáfrica, 2000.
La divulgación pública de recursos minerales, requiere que las estimaciones se clasifiquen según grados de confianza y se subdividan como recursos medidos, indicados e inferidos.
Es de saber que los recursos medidos son los que entregan la menor incertidumbre en su estimación y que posteriormente podrán convertirse en reservas (volumen mineralizado de carácter económico).
La decisión de invertir en un proyecto considera la confiabilidad en los valores estimados de estos recursos (Wober and Morgan, 1993). En la definición del grado de confiabilidad, surge la subjetividad de las técnicas aplicadas para definir estas categorías.
Varios aspectos son considerados al definir la calidad del valor estimado, siendo las más comunes:
El grado de continuidad geológica que el experto considera existe en la mineralización.
La cantidad de información disponible y su configuración geométrica.
El grado de continuidad espacial de las leyes, el cuál es medido a través de la geoestadística.
De este último punto, las técnicas geoestadísticas de estimación permiten estimar la ley de bloque de manera óptima, en el sentido que se minimiza la varianza de estimación.
La varianza mínima resultante se conoce como la varianza de estimación de kriging (Emery, 2000).
FUNDAMENTOS:
De manera de hacer más comprensible el formulismo, acotaremos los conceptos de estimación geoestadística y varianza de estimación de kriging, a puntos.
La hipótesis inicial es que el estimador [Z*(x)] de un punto, esta afecto a una desviación potencial, ε, de su valor real [Z(x)].
ε = [Z(x) – Z*(x)]
Donde:
- ε: error de estimación
- Z(x): valor real
- Z*(x): valor estimado
Por ende, entre más cercano a cero es el error, mayor confiabilidad tendrá el método de estimación para [Z*(x)].
Si ε = 0; entonces Z(x) = Z*(x)
El error se suele calcular como ε² (error cuadrático), para penalizar de forma igualitaria:
ε² = [(Z(x) – Z*(x))²]
Luego la varianza (S²) en términos prácticos, la definiremos como la esperanza (E) del error cuadrático:
S² = E[(ε – me) ²] = E[ε ²]
S² = E[(Z(x) – Z*(x)) ²]
Si S² = 0; entonces Z(x) = Z*(x)
Resumiendo, podemos decir que el valor real de un punto de interés [Z(x)], se expresa como el valor estimado [Z*(x)] más su respectiva varianza [S²]:
Z(x) = [Z*(x) + S²]
El método geoestadístico denominado Kriging Simple, funciona conociendo un momento de segundo orden (covarianza) y un valor medio global que afecta a la unidad a estudiar. Por esto último es que también es llamado Kriging de la media por algunos especialistas.
El estimador de Kriging Simple (SK), se presenta de la siguiente forma:
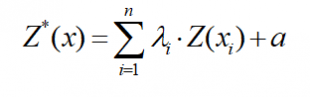
Donde:
- Z*(x): Estimador KS
- Z(xi): valor del punto dentro de la zona de influencia (muestra conocida)
- λi: ponderación asignada a la muestra conocida
- a: producto entre la media global (m) y su ponderador
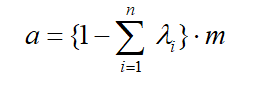
Luego también podemos expresar el estimador de Kriging Simple como:
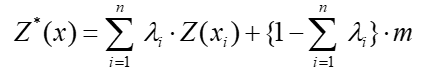
Una de las cualidades de este estimador geoestadístico es que es insesgado, por ende la sumatoria de los ponderadores [λi] debe igualar a uno:
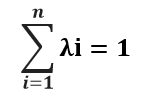
De esto último es que se entiende la restricción para “a”, que asume una ponderación que complementa la asignada a las muestras conocidas.
Anteriormente se mencionó que el Kriging Simple trabaja conociendo la covarianza, la cual es un estadístico bivariable que analiza la dependencia entre las muestras conocidas [Z(xi)] y [Z(xi+h)], y las mismas a la ubicación a estimar [Z(xi)] y [Z*(x)].
Donde:
- Z(xi): valor de la variable en la ubicación “xi”
- Z(xi+h): valor de la variable en la ubicación “xi” desplazada en un vector “h”.
- Z*(x): valor a estimar en la ubicación “x”
Al tener la covarianza [C(h)], entre las muestras y las mismas al punto a estimar, es que se puede formar un sistema matricial o un sistema de ecuaciones que resulten en la obtención de los ponderadores [λi] que requiere el estimador [Z*(x)] de KS.
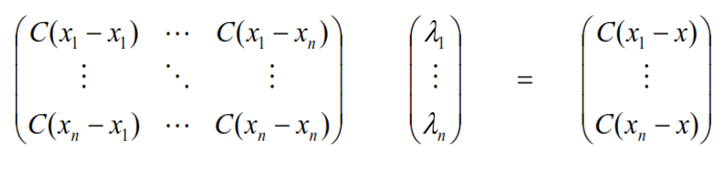
Del sistema anterior se entiende que C(x1 – xn) es la covarianza que existe entre la muestra conocida y ubicada en el punto “x1” y la muestra ubicada en el punto “xn”. Luego C(x1 – x), será la covarianza que exista entre la muestra ubicada en el punto “x1” y el punto a estimar “x”.
A su vez la covarianza se puede obtener a partir del variograma (herramienta fundamental de la geoestadística):
C(h) = [C(0) - γ(h)]
Donde:
- C(h): covarianza
- C(0): covarianza en h = 0; varianza o meseta
- γ(h): varianza en h

Al desarrollar el sistema de ecuaciones con las covarianzas, se obtendrán los ponderadores de las muestras [λi] que influyeron en la estimación de [Z*(x)]. Con esto ya se podrá dar solución al problema de la estimación.
Luego se puede pasar a calcular la varianza de estimación del Kriging Simple, mediante la siguiente formula:
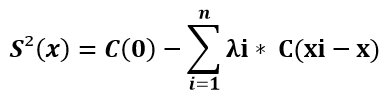
Donde:
- S²(x): varianza de estimación de Kriging Simple
- C(0): covarianza en h = 0
- λi: ponderación asignada a la muestra conocida
- C(xi –x): covarianza entre la muestra conocida y punto a estimar
A estas alturas, es destacable considerar que tanto los ponderadores y la varianza de kriging toman en cuenta:
Aspectos geométricos: distancias entre el sitio a estimar y los datos; distancias (redundancias) entre los datos mismos.
Aspectos variográficos: continuidad espacial, anisotropía, mediante la covarianza o el variograma.
Luego de haber presentado el formulismo del estimador [Z*(x)] y su varianza de estimación [S²(x)], vamos a retomar el concepto del error [ε] que es la base para el propósito de la categorización de recursos.
Asumiremos que la distribución de los valores [Z(x) – Z*(x)] es una distribución normal, la desviación ε de los valores [Z*(x)] puede ser expresada en función de un nivel de confianza seleccionado.
Así, podríamos decir que para un 95% de confianza, la desviación se transforma en 1.96*S, que para un 90% de confianza se transforma en 1.64*S, y que para un 85% de confianza se transforma en 1.44*S.
De este modo, digamos que para un nivel de confianza “f”, la desviación se transforma αf*S, siendo “α” función del nivel de confianza “f” seleccionado. Así finalmente para un nivel de confianza f:
ε Z*(x) = αf*S
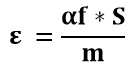
Esta fórmula se presenta en estadísticas como el coeficiente de variación [CV], expresa la desviación estándar como porcentaje de la media, mostrando una mejor interpretación porcentual del grado de variabilidad que la desviación estándar [S].
Por otra parte, establezcamos una función de categorización K con tres estados, esto es, para K(M) = recurso medido, K(ID) = recurso indicado, y para K(IF) = recurso inferido.
Debe existir correspondencia entre esta función y la desviación relativa [S/Z*(x)], asociada con estas tres categorías.
Asumamos que la desviación está asociada a tres valores seleccionados [S/Z*(x)] (M), [S/Z*(x)] (ID), [S/Z*(x)] (IF). Así:
![]()
Se podría decir, por ejemplo, que de acuerdo a requerimientos productivos y condiciones operativas:
- Para K(M) se ha establecido un nivel de desviación [S/Z*(x)] (M) menor al 20%
- Para K(ID) se ha establecido un nivel de desviación [S/Z*(x)] (ID) entre 20 % y 50%
- Para K(IF) se ha establecido un nivel de desviación [S/Z*(x)] (IF) mayor al 50%
En otras palabras:
K(M) 0.00 ≤ S/[Z*(x)] < 0.20
K(ID) 0.20 ≤ S/[Z*(x)] ≤ 0.50
K(IF) 0.50 < S/[Z*(x)] ≤ 1.00
Con esto finalmente podemos categorizar el punto estimado en función a su error de estimación.
EJEMPLO:
Se requiere estimar un punto en el espacio a partir de dos muestras conocidas y cercanas. Luego definir la confiabilidad en la estimación a partir de la varianza de estimación y categorizar si corresponde a un recurso medido, indicado o inferido:
Datos:
- Ubicación de las muestras y punto a estimar:
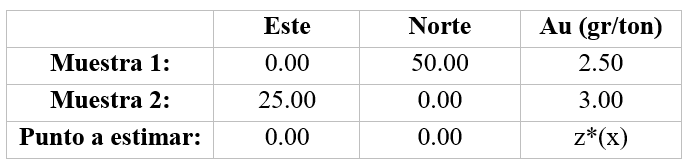
- Modelo estructural: γ(h) = SPH(h/120)
- Media global: 3.2 gr/ton Au
Desarrollo:
- Calculo de distancias:

- Calculo de varianzas de dispersión:

- Calculo de covarianzas:

- Sistema de ecuaciones con C(h):
1λ1 + 0.35λ2 = 0.41
0.35λ1 + 1λ2 = 0.69
Luego; λ1 = 0.19; λ2 = 0.62
- Ponderadores:
Sumando λ1 + λ2 = 0.81
Luego:
a = (1 – 0.81)*3.2
- Resumiendo con los ponderadores:
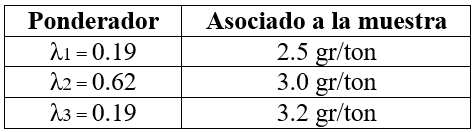
- Estimando Z*(x): Kriging Simple
Z*(x) = [(0.19*2.5) + (0.62*3.0) + 0.19*3.2)] = 2.94 gr/ton Au
- Estimando S²(x): Varianza de estimación de Kriging Simple
S²(x) = 1 – [(0.19*0.41) + (0.62*0.69)] = 0.49
- Estimando S(x): Desviación de estimación de Kriging Simple
S(x) = √0.49 = 0.70
- Estimando el error de estimación KS:
Error = 0.70/2.94 = 0.24
- Categorizando:
K(M) 0.00 ≤ S/[Z*(x)] < 0.20
K(ID) 0.20 ≤ S/[Z*(x)] ≤ 0.50
K(IF) 0.50 < S/[Z*(x)] ≤ 1.00
- Categorizando con un nivel de confianza del 90%:
Error (90% de confianza) = (0.70*1.64)/2.94 = 0.39
Finalmente el recurso estimado [Z*(x)] corresponde a un recurso indicado.


Debe estar conectado para enviar un comentario.