
En el presente artículo se presenta una implementación en Python de la técnica clustering jerárquico (Hierarchical Clustering en inglés), en la definición de dominios de estimación para variables geo-mineras. El clustering o agrupamiento es una técnica de aprendizaje automático no supervisado, cuyo objetivo es ordenar objetos definidos por un conjunto de variables en grupos, de forma que los elementos sean lo más homogéneos posibles.
En minería, la caracterización de los diferentes sectores de un depósito de acuerdo a sus atributos geológicos y estadísticos más relevantes, así como la discriminación de poblaciones de acuerdo a sus litologías, mineralogías, grados de alteración y contenidos en mineral, constituye la fase más crucial en el análisis de yacimientos mineros (Tulcanaza, 1999). Los dominios de estimación son el equivalente geológico a las zonas de comportamiento estacionario y se definen como un volumen de roca con controles de mineralización que resultan en distribuciones aproximadamente homogéneas (Rossi y Deutsch, 2014). La definición y el modelado de estos dominios es un paso de suma importancia en la estimación de recursos minerales, dado que la correcta partición del depósito mineral en poblaciones homogéneas, disminuirá el sesgo condicional característico de la estimación geoestadística.
Entendiendo lo anterior resulta atractivo el estudiar la técnica de clustering jerarquico, dentro del contexto de la evaluación de depósitos minerales. Es por ello que se construye un caso sintético, que cumple parcialmente las características de una muestra minera resultante de un proceso inicial de prospección., que consta de 49 observaciones para 3 variables; cobre (Cu), oro (Au) y tipo de roca (ROCK), repartidas en el plano cartesiano a través de una malla cuadrada de 250 x 250 m.
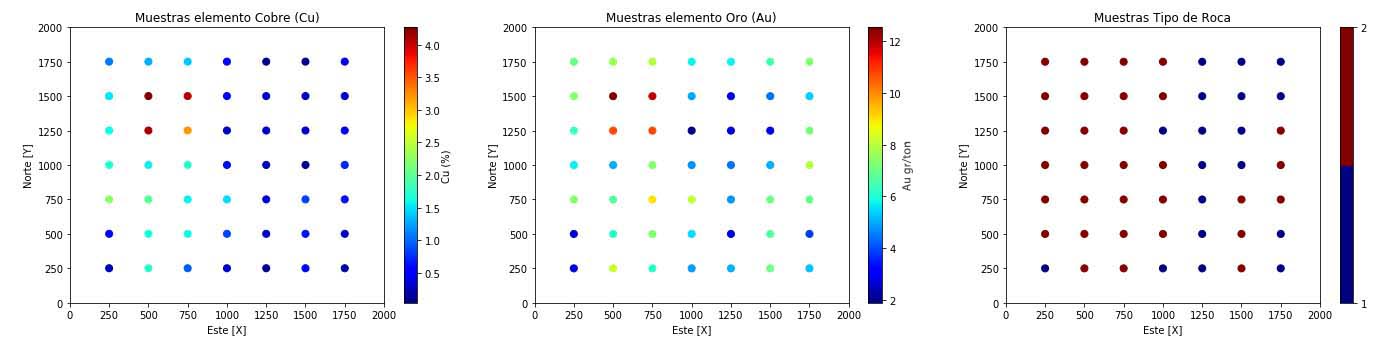
Figura 1. Mapa muestras Cu, Au, tipo de roca.
Con letra X se expresa la variable, donde:
![]()
La idea principal es poder relacionar las observaciones de estas tres variables, en búsqueda de agrupar las muestras con menor disimilitud conjunta. Para ello se cuenta actualmente con una serie de mediciones con distintas características. Por ejemplo la biblioteca de Python Scikit-learn, posee hasta 22 tipos de distancias para medir la disimilitud entre muestras. Algunas de ellas son:
- Distancia Euclidiana
- Distancia rectilínea o Manhattan
- Distancia Minkowski
- Distancia Coseno
- Distancia Mahalanobis
- Distancia Kulczynski
En este caso se utiliza la distancia Euclidiana que se presenta como:
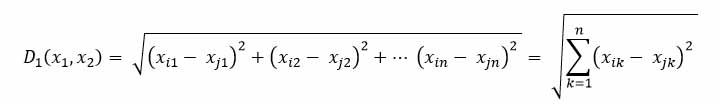
Por ejemplo midiendo la distancia entre la muestra 1 y 2, obtenemos:
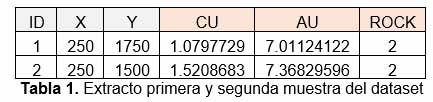

Sin embargo cuando se tienen variables con distinta escala, es recomendable el estandarizarlas previamente. En este caso el Cu, Au y tipo de roca, son estandarizadas mediante la siguiente formula:
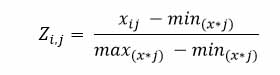
La observación mínima toma un valor “0”, mientras que la observación máxima un valor de “1”., luego se calcula la distancia en todas las combinaciones posibles. Al ser 49 muestras, la cantidad de distancias euclidianas calculadas son 2,401, las que son representadas a través de una matriz de tamaño 49 x 49.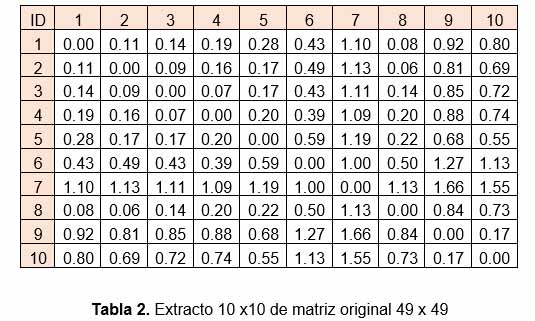
En este caso para agrupar las muestras en dominios homogéneos, se utiliza un clustering jerárquico aglomerativo, sin embargo es importante señalar que existen dos categorías para métodos jerárquicos; aglomerativos y disociativos. Los métodos aglomerativos, también conocidos como ascendentes, comienzan el análisis con tantos grupos como individuos haya. A partir de estas unidades iniciales se van formando grupos, de forma ascendente, hasta que al final del proceso todos los casos tratados están englobados en un mismo conglomerado. Los métodos disociativos, también llamados descendentes, constituyen el proceso inverso al anterior. Comienzan con un conglomerado que engloba a todos los casos tratados y, a partir de este grupo inicial, a través de sucesivas divisiones, se van formando grupos cada vez más pequeños. Al final del proceso se tienen tantas agrupaciones como casos han sido tratados.
Adicionalmente al cálculo de distancias entre muestras, la aplicación del análisis cluster requiere de la determinación de las distancias entre los grupos, para ello es que existen varias alternativas, entre algunas; agrupamiento mínimo (enlace simple), agrupamiento máximo (enlace completo), y agrupamiento promedio (enlace promedio), la cual es implementada en este caso.
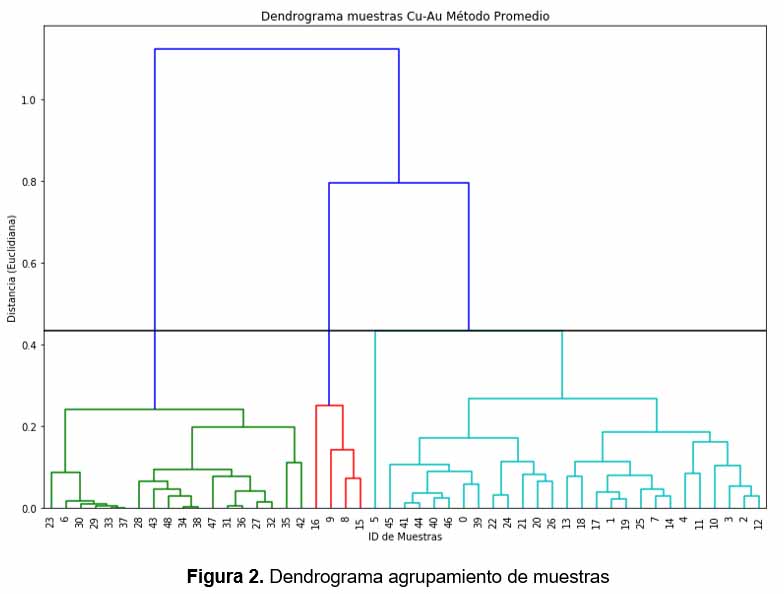
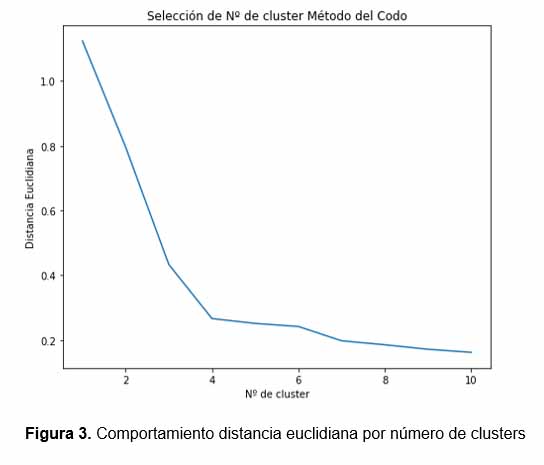
La representación gráfica del resultado se genera a través de un Dendrograma (figura 2), y la selección del número de agrupamientos en este caso, depende del método denominado del “codo”, el cual básicamente analiza los cambios de disimilitud por número de agrupamientos (figura 3).
El resultado puede ser visualizado por muestra, en un mapa georreferenciado para cada variable (figura 4) y en un diagrama de dispersión Cu-Au (figura 5).
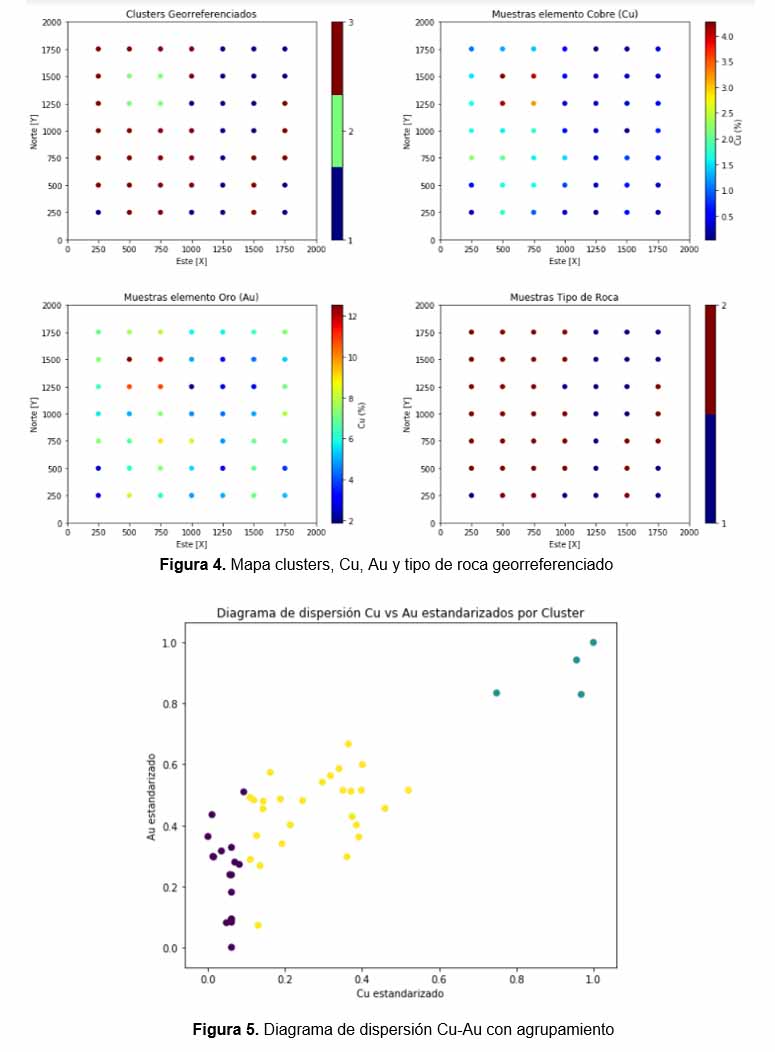
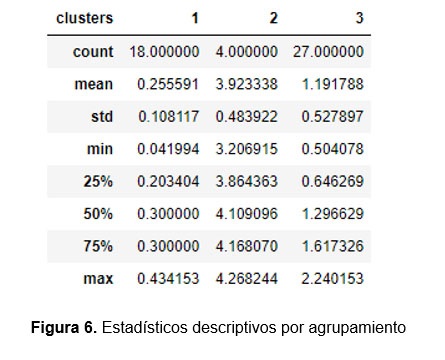
Finalmente se concluye que el número de clusters adecuado para esta muestra, es de tres, y se recomienda continuar la prospección en el cluster con mayor contenido mineral (cluster número 2), previo a un proceso de estimación.
Dataset utilizado: samples_clustering


Debe estar conectado para enviar un comentario.