Una pregunta recurrente en la estimación de recursos minerales es:

¿Cuál es la mejor alternativa para estimar la ley mineral en lugares donde no existe muestra?

A priori lo que se viene a la cabeza es utilizar un modelo geoestadístico, dado que está ampliamente validado por explotar la correlación espacial, a favor de mejorar los procesos de estimación. Ahora, esta elección no puede ser tomada a la ligera y ha de cuestionar si la ley mineral que deseamos estimar cumple a nivel de muestra con los requisitos en el uso de estas técnicas, inclusive particionando su distribución por dominios.

En este breve artículo revisaremos el concepto de estacionaridad como base para la modelización estructural y estimación geoestadística lineal.

Ha de recordar que la geoestadística definida por su fundador G. Matheron (1962), es la teoría de las variables regionalizadas a la estimación de procesos o fenómenos geológicos en el espacio.

Pero ¿Qué es una variable regionalizada?. Es una variable que se extiende en el espacio geográfico y presenta una cierta continuidad. Conceptualmente se define como una realización de una función aleatoria (FA), donde esta última corresponde a un conjunto de variables aleatorias espacialmente distribuidas.

La función aleatoria (FA) es caracterizada por su función de distribución de probabilidad n-variada:

Y a su vez resumida de manera práctica en los dos primeros momentos. La esperanza matemática de primer orden:

La varianza, la auto covarianza y el semivariograma, como momentos de segundo orden:

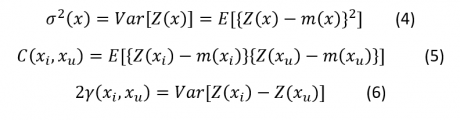
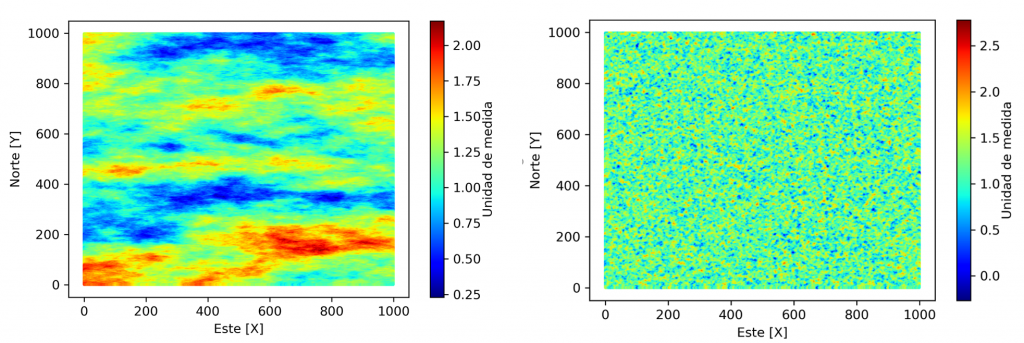
Figura 1. Ejemplo en un espacio 2D de variable regionalizada (izquierda) y no regionalizada (derecha)

Si bien la ley mineral es considerara perse una variable regionalizada, hay casos de elementos como el oro (Au), que, en ciertas circunstancias geológicas, no satisfacen los requerimientos del modelo geoestadístico, dado principalmente a su alta variabilidad y dificultad en la modelización por la casi nula continuidad espacial a nivel de muestra. En el caso de que una ley mineral no tenga autocorrelación, se distribuya espacialmente de forma errática sin evidenciar alguna estructura espacial modelable, inclusive de forma local, y no sea posible restringir un dominio estacionario. Es que ha de buscar una mejor manera de estimar a partir de esa muestra y olvidar la geoestadística lineal.

Pero ¿Qué es la estacionaridad?.  Se dice que una función aleatoria es estrictamente estacionaria, cuando su función de distribución de probabilidad es invariante a cualquier traslación respecto a un vector h. Dicho de otra forma, es cuando en un dominio la ley mineral no varia por traslación. Es decir, la función de distribución del vector aleatorio {Z(x_1 ),Z(x_2 ),…,Z(x_n )} es idéntica a la del vector {Z(x_1+h),Z(x_2+h),…,Z(x_n+h)} para cualquier h. Esta hipótesis de forma conveniente es limitada a los dos primeros momentos de la función aleatoria, empleándose el concepto de estacionaridad de segundo orden. Gráficamente se puede ver en la siguiente figura donde la ley media mineral y su varianza permanecen constante en el espacio (1D).

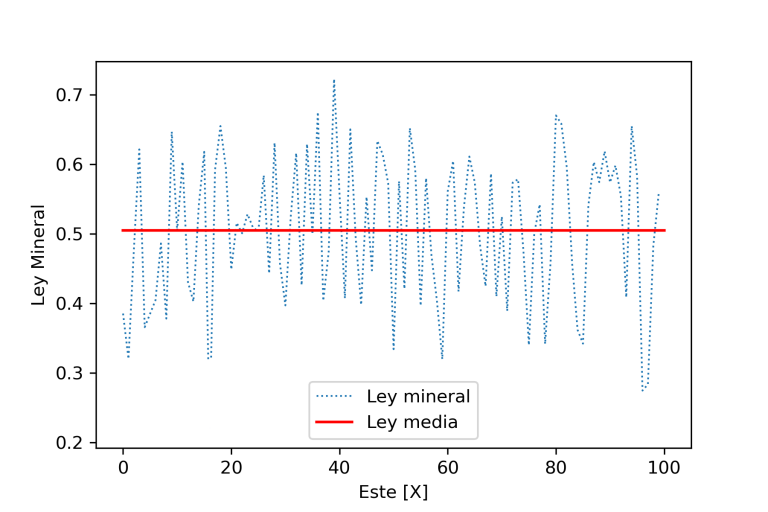
Figura 2. Concepto de estacionaridad en un gráfico de líneas

Es importante señalar que existen distintos grados de estacionaridad, algunos mas fuertes y muy estrictos, y otros más débiles y nulos:

– FA con estacionaridad estricta

– FA con estacionaridad de segundo orden

– FA con casi estacionaridad de segundo orden (estacionariedad local)

– FA no estacionaria de segundo orden, pero con hipótesis intrínseca

– FA no estacionaria

Para efectos prácticos en la aplicación de la geoestadística, ha de cumplirse por lo menos una estacionaridad de segundo orden.  También es necesario señalar que no basta con aprobar la estacionaridad en base a la figura 2 donde se presenta el comportamiento de la variable en el espacio, sino que debe usarse además un gráfico de semivariograma para descartar tendencia entre las diferencias [Z(x)-Z(x+h)].

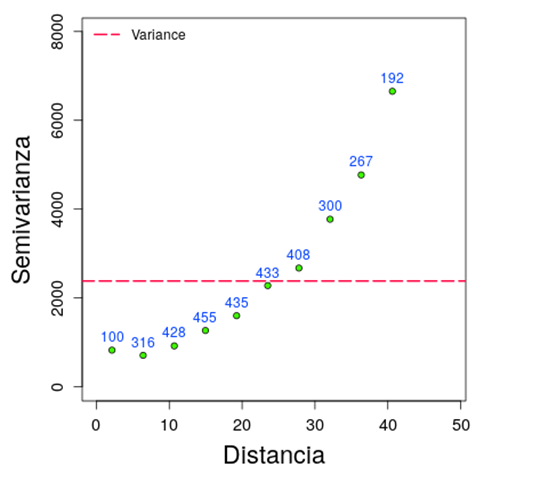
Figura 3. Ejemplo de tendencia en el semivariograma experimental

Diríamos entonces que en la estacionaridad práctica ha de cumplirse que:

– La ley media mineral no dependa de la ubicación y no se presencie tendencia.

– La varianza de la ley mineral no dependa de la ubicación y no se presencie tendencia.

– Para todos los vectores «h», la varianza de la diferencia [Z(x)-Z(x+h)] no dependa de la ubicación, y no se presencie tendencia en la varianza local de las diferencias.

Para finalizar es que señalaremos que la estacionaridad no es una propiedad de la ley mineral, si no que es una decisión. Una decisión de separar nuestros datos y agruparlos de tal forma que se cumpla la estacionaridad. La escala en la que se estudie el comportamiento de la ley mineral también jugara un rol importante en la estacionaridad, dado que es conocido que entre mas lejanas se encuentren las observaciones de una muestra, mayor será su disimilitud. Por lo tanto, a escala mas pequeña, mayor probabilidad de estacionaridad.