
En el desafío de interpretar el comportamiento de una variable espacial, en lugares donde esta no ha sido medida, recurrimos a estudiar distintos modelos de interpolación, que logren a partir de información fragmentaria (muestra), estimar lo mejor posible la realidad de dicha variable.
Por ejemplo, en la provincia de Viscaya en España, existen 20 estaciones de monitoreo instaladas para medir contaminantes en el aire. Esta provincia esta compuesta por 112 municipios y es la tercera mas densa en población del país. El problema se resume en estimar los contaminantes de forma diaria en los 2,217 km² que posee de área la provincia. Diríamos que una variable espacial de interés es el PM10 y que tenemos 20 datos puntuales para interpretar el nivel de contaminación en una considerable cantidad de lugares en donde esta no ha sido medida.
¿Qué modelo de interpolación espacial escoger?
Un método para evaluar el o los modelos que estemos implementando en la interpolación, es la denominada validación cruzada dejando uno fuera, mayormente documentada en inglés como leave one out cross validation.
¿Cómo funciona este método de validación?
Básicamente, divide nuestros datos medidos en un conjunto de entrenamiento y un apartado único de prueba, tantas veces como numero de datos tengamos. Secuencialmente se saca una de las mediciones conocidas, y se estima en dicha ubicación espacial con el modelo. De esta forma se puede comparar el valor que estima el modelo versus el valor verdadero de la variable.

Luego el promedio del error cuadrático funciona como indicador para comparar distintos modelos y quedarse con el que menor error posea. Gráficamente la validación cruzada se puede presentar a través de un diagrama de dispersión entre la variable estimada y la real.
Veamos un ejemplo preparado para entender de mejor manera el funcionamiento de la validación cruzada dejando uno fuera.
Ejemplo desarrollado en Python: Caso sintético 2D
Con uno de la simulación geoestadística se plantea un escenario para la variable sintética denominada VS. Esta a simple vista presenta dependencia espacial, no es una variable que se comporte de forma errática en el espacio, mas bien presenta una estructura.
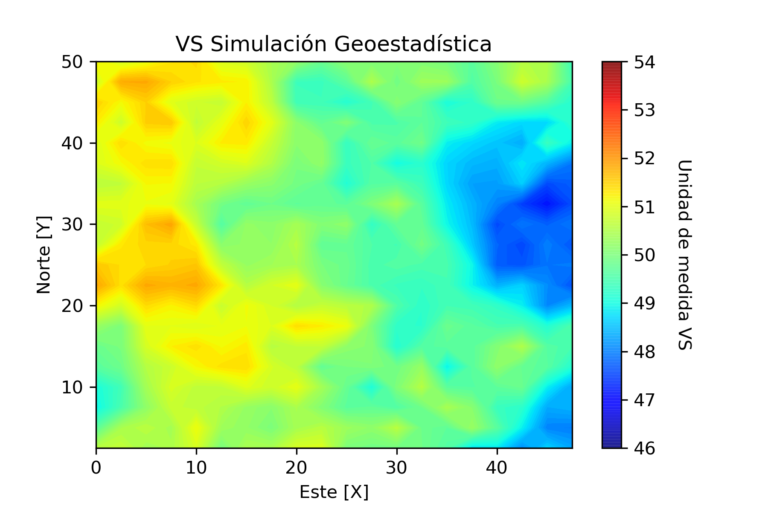
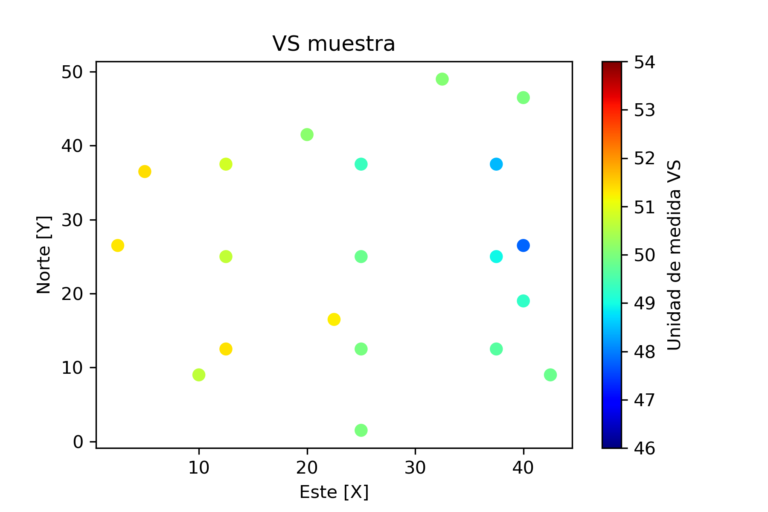
De este escenario base, es que se extraen 20 mediciones de VS.
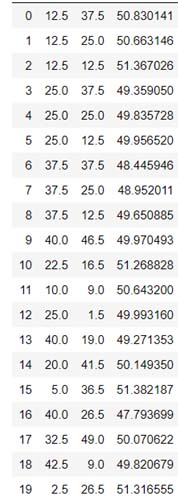
De la siguiente tabla de datos correspondiente a las muestras , la primera columna corresponde al No de la medición (inicia en 0), la coordenada en X, coordenada en Y, y en la ultima columna el valor que toma la variable en dicha ubicación.
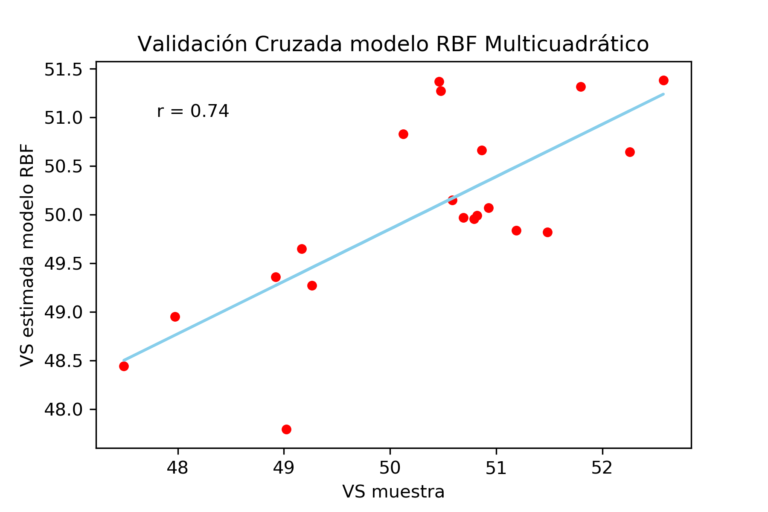
El modelo propuesto en este caso es una función de base radial del tipo multicuadrático, mayormente documentado en inglés como RBF multiquadric.
El resultado de la validación cruzada es bueno, los valores interpolados con el modelo se acercan bastante a los reales y esto queda expuesto con un coeficiente de correlación lineal del 74%.
¿Podría mejorar utilizando otro modelo distinto al RBF multicuadrático?
Pues podría, o no también. Es cosa de probar.
¿Es confiable el método de validación cruzada para evaluar la precisión del interpolador espacial que estemos implementando?
De esto existe una discusión ya de años, y no es un método en el que debamos confiar al 100%. Supongamos que el resultado de la validación cruzada es perfecto, los valores estimados son idénticos a los reales. Esto ultimo no asegura que se tenga la misma precisión para interpolar en otros puntos.
En el ejemplo que hemos planteado, tenemos una variable simulada que vendría a ser nuestra realidad. Por ende, bien podemos relacionar la totalidad de datos simulados versus la misma cantidad de datos interpolados con el modelo, y calcular un coeficiente de correlación lineal que podamos comparar con el obtenido de la validación cruzada.
¿Qué software poseen este algoritmo de validación cruzada?
Si bien son varios, todos de pago (software comercial), personalmente me gusta Supervisor de Swowden Group. En el siguiente enlace existe información y un ejemplo de su uso: https://snowdengroup.com/news/supervisor-8-5-cross-validation/
Finalmente comento que compartiré un código en Python preparado para la validación cruzada de autoría propia en el séptimo modulo del curso Modelado de datos espaciales en Python (ADEP), en donde también se detalla en la explicación y se evalúa a su vez la precisión del método de validación cruzada.


Debe estar conectado para enviar un comentario.