DESAGRUPAMIENTO DE DATOS MEDIANTE MÉTODO DE CELDAS
EJEMPLO 3D USANDO DATAMINE SUPERVISOR
Escrito por Heber Hernández G. (Junio, 2021)

Contenidos
En este breve artículo, hablaremos sobre el desagrupamiento de datos mediante el método de celdas y como implementarlo sobre un caso 3D usando DATAMINE SUPERVISOR.
Ha de saber que en una campaña prospectiva de minerales, las muestras rara vez son recogidas de forma aleatoria, sino más bien, son dirigidas en áreas que poseen un mayor interés geológico.
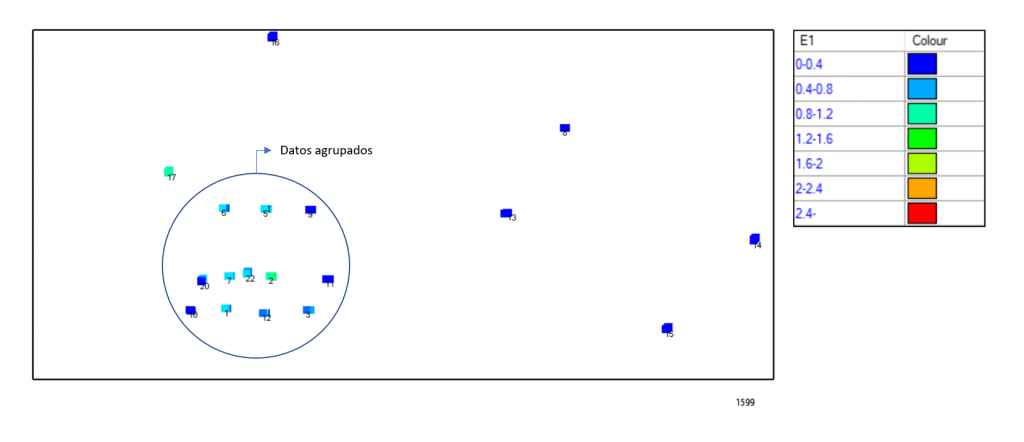
Figura 1. Vista superior ley mineral E1 (sección XY cota 1599)
Por ejemplo, en la figura 1 observamos que los datos se agrupan donde las concentraciones de mineral son más altas, lo cual conduce a que el muestreo sea preferencial o sesgado. Esto ultimo se da en la mayoría de las industrias que recopilan datos espaciales, es totalmente aceptable y tiene una justificación técnico -económica. Lo importante es que debemos considerarlo, es decir debemos prestarle atención al carácter espacial de los datos, antes de tomar decisiones directamente con ellos.
¿QUÉ PASARÍA SI NO CONSIDERAMOS EL CARÁCTER ESPACIAL DE LOS DATOS?
Podríamos estar cometiendo errores al obtener estadísticos directamente de la muestra, y así afectar nuestra toma de decisión. Como ejemplo tomaremos un grupo de sondajes pertenecientes a un mismo dominio geológico y en donde podemos ver la existencia de un agrupamiento de datos.

Figura 2. Vista isométrica ley mineral E1
Como se observa en la figura 2, el agrupamiento representa solo una porción del volumen y preferentemente las concentraciones de la ley mineral, son mas altas que en aquellos sectores donde los datos están menos muestreados.
Si consultamos la ley media de la muestra, esta es de 0.45% e implícitamente se encuentra sobre estimada para el volumen a nivel general, es decir esta ley no es representativa.
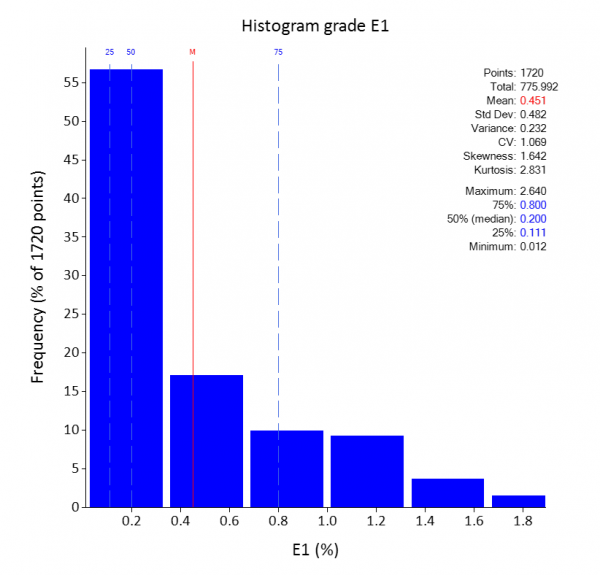
Figura 3. Histograma ley mineral E1
Pero tranquilidad, debemos saber que existen métodos dedicados a desagrupar datos geoespaciales sesgados y así lograr estadísticas más representativas, que aproximen mejor la distribución de la variable de interés y nos ayuden a tomar mejores decisiones.
¿QUÉ SIGNIFICA DESAGRUPAR DATOS GEOESPACIALES?
En palabras muy simples, es asignar un peso a cada ley mineral, donde aquellas leyes que se encuentren agrupadas serán castigadas con menos peso y viceversa, las leyes aisladas tendrán una mayor influencia teniendo asignado un peso mayor. Los pesos serán mayores que 0 y deberán sumar 1.
Por ejemplo, la ley media y desviación estándar desagrupada son obtenidas de la siguiente forma:
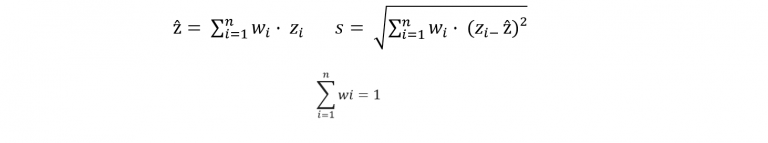
Ha de considerar que existen distintos métodos de desagrupamiento, sin embargo el más popular es el método de celdas, presentado por André Journel en 1983, para luego ser modificado en 1989 por Clayton Deutsch, es más, el famoso contenedor de sofware de código abierto GSLIB, acrónimo de Geostatistical Software Library, incorpora el programa de desagrupamiento por método de celdas (DECLUS), junto con otros programas producto de los trabajos de Journel y Deutsch durante los años 90 en la Universidad de Stanford.
¿CÓMO SE ASIGNAN LOS PESOS EN BASE AL MÉTODO DE CELDAS PROPUESTO POR DEUTSCH?
El desagrupamiento mediante celdas funciona de la siguiente manera:
– Se divide el volumen de interés en una cuadricula de celdas L = 1, …, n.
– Se cuentan las celdas ocupadas (Lo) y la cantidad de datos en cada celda ocupada (nl).
– Se pondera cada dato de acuerdo con la cantidad de datos que caen en la misma celda, por ejemplo, para el dato “i” que cae en la celda “L”, el peso de la celda que se desprende es:
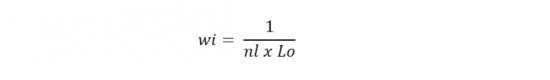
A cada celda ocupada se le asigna una ponderación (peso). Una celda desocupada simplemente no recibe ninguna ponderación. Una descripción más profunda y varios ejemplos podrá encontrar en (Deutsch, pg. 50-63, 2002).
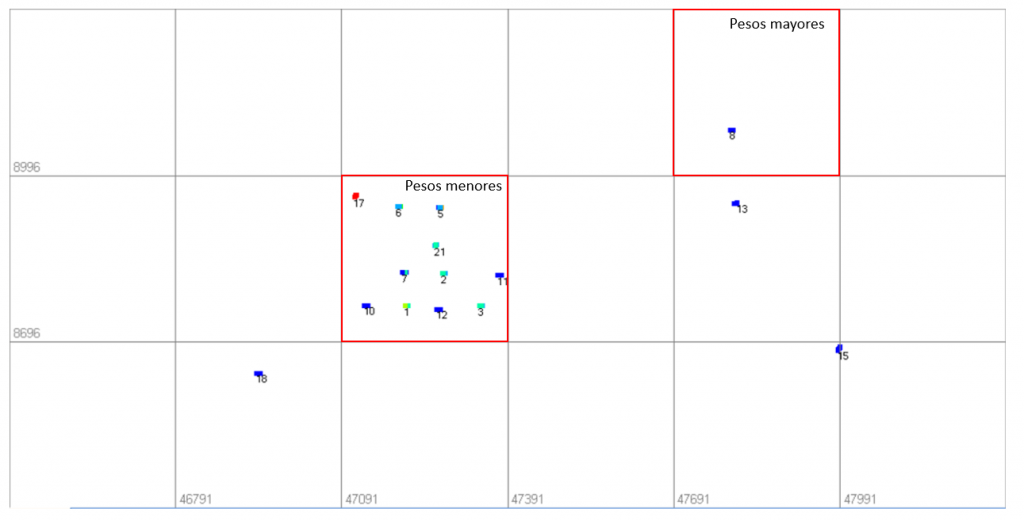
Figura 4. Vista superior sistema de celdas 300 x 300
¿CÓMO SABER QUE TAMAÑO DE CELDA ES ÓPTIMO?
Antes de responder esta pregunta, es necesario saber que cuando el tamaño de la celda es muy pequeño, cada dato está en su propia celda y recibe el mismo peso. Cuando el tamaño de la celda es muy grande, todos los datos caen en una celda y se ponderan por igual. Entonces el seleccionar un tamaño de celda adecuado es clave para desagrupar nuestros datos de buena manera.
La forma es muy simple, se crea un gráfico donde es estimada la ley media desagrupada a distintos tamaños de celda. El tamaño optimo es cuando se mínima o maximiza la media desagrupada, es decir van a existir casos como el que estamos presentando donde el agrupamiento concentre leyes altas y en este caso se buscará minimizar. Si el agrupamiento concentrara leyes bajas, buscaríamos maximizar.

Figura 5. Media desagrupada vs tamaño de celda (3d volumen)
En la figura 5 se puede apreciar que para cuando la celda en XY es de 300 x 300, los 150 m en Z resulta el mas adecuado, dado que mínima la ley media.
¿EL ALGORITMO DE DESAGRUPAMIENTO DE CELDAS DE SUPERVISOR SIGUE AL PIE DE LA LETRA EL MÉTODO PROPUESTO POR DEUTSCH?
Si bien sigue los mismos principios, el algoritmo de Supervisor asigna los pesos de acuerdo a la siguiente formula:
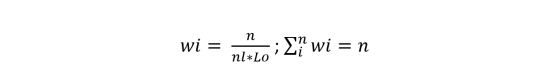
Donde n es el número total de datos, lo que resulta en una normalización donde la media de los pesos siempre será 1, mientras que la sumatoria de los pesos será n. Esto ultimo se puede observar en el histograma de los pesos en la figura 6.
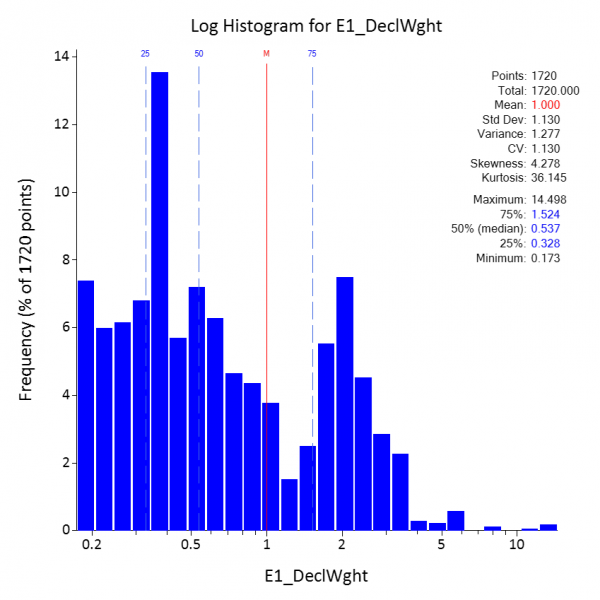
Figura 6. Histograma de pesos lognormales resultantes del desagrupamiento de celdas
Finalmente la idea es comparar los histogramas de los datos antes y después del desagrupamiento, en este caso la media disminuye consecuencia de que leyes bajas aumentaron su influencia. La dispersión también disminuye estando las leyes en general más cercanas a la media y la curtosis aumento, esto último se aprecia en el histograma de la ley ya desagrupada, donde existe un apuntalamiento en el rango entre 0.1 y 0.2 % que concentra aproximadamente un 35% del total de datos.
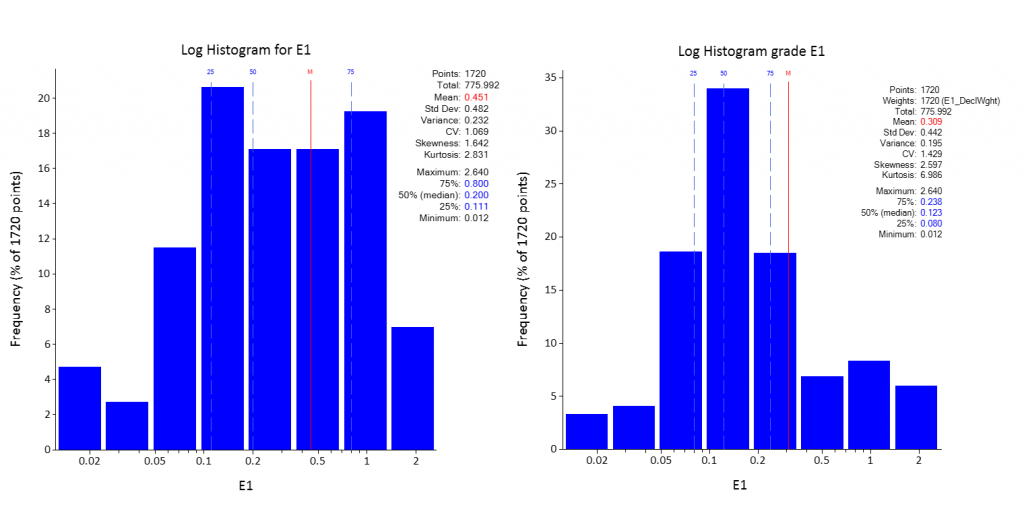
Figura 7. Histograma para Log ley mineral vs Log ley mineral desagrupada
¿QUÉ HERRAMIENTAS EXISTEN PARA REALIZAR EL DESAGRUPAMIENTO DE DATOS 3D?
Hablando de software libre y código abierto, se encuentra la antes señalada GSLIB, considerada por algunos autores como el principal desarrollo informático en la historia de la Geoestadística (Remy, 2009), y en la cual encontramos el algoritmo DECLUS. Luego podemos ver reimplementado este algoritmo a través de scripts en las versiones gratuitas del software SGeMS, acrónimo de The Stanford Geostatistical Modeling Software. Y si bien esto suena bastante bien, existen limitaciones que podrían frenar nuestro entusiasmo. Por ejemplo, en GSLIB y SGeMS se puede realizar un desagrupamiento de celdas, pero no se puede generar el análisis de escenarios y postproceso estadístico, entonces ha de tener algunas nociones en programación y terminar la tarea escribiendo algo de código. Es importante señalar que estas soluciones fueron creadas en la academia y para su uso con fines pedagógicos o de investigación.
Ahora si el propósito es dedicarse exclusivamente a los datos y buscar una curva de aprendizaje mucho más corta, es que las soluciones que ofrecen las empresas desarrolladoras de software geológico minero resultan el camino mas elocuente, es decir, es mucho más intuitivo su uso y existen herramientas a disposición con algoritmos operando a partir de un mínimo de instrucciones.
Es por eso que en esta oportunidad se ha usado SUPERVISOR, gentileza de la empresa DATAMINE, con el cual se ha preparado el ejemplo y realizado un desagrupamiento de datos 3D en cosa de minutos. El programa en si es una herramienta muy potente en análisis estadístico y geoestadístico aplicado a la estimación de recursos, amigable en su interfaz y con una serie de herramientas novedosas que esperamos probar y comparar más adelante.
¿CÓMO REALIZAR EL DESAGRUPAMIENTO 3D EN SUPERVISOR DATAMINE?
En el siguiente video podrás ver brevemente como es que en solo algunos minutos tenemos ya un desagrupamiento de celdas sobre un caso 3D.
REFERENCIAS
Deutsch, Clayton (2002). Geostatistical Reservoir Modeling.
Deutsch. DECLUS: A Fortran 77 program for determining optimum spatial declustering weights. Computers & Geosciences, 15(3):325–332, 1989.
Journel, A. G. (1983). Nonparametric estimation of spatial distributions: Jour. Math. Geology, v. 14, no. 3, p. 445- 468.
Remy, N.; Boucher A. y W. Jianbing (2009). Applied Geoestatistics with SGeMS; A User’s Guide. Cambridge University Press. New York.
