
En una campaña prospectiva de minerales, las muestras rara vez son recogidas de forma aleatoria, sino que más bien, son dirigidas en áreas que poseen un mayor interés geológico.
La práctica de recolectar más muestras en áreas de alta concentración del elemento de interés, no debe ser modificada, ya que conduce a un aumento de datos en porciones del sector realmente importante. Sin embargo, es necesario realizar algunos ajustes para que los histogramas y estadísticas descriptivas de los datos sean representativas de todo el volumen de interés.
Esto último se entiende, dado al agrupamiento de muestras en sectores privilegiados, que resultan en una malla irregular.
Las técnicas de desagrupamiento asignan a cada dato, una ponderación basada en la cercanía a las muestras circundantes wi, i = 1, …, n. Estas ponderaciones son mayores que 0 y suman 1.
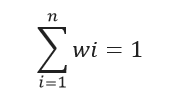
La distribución experimental y todas las estadísticas de resumen se calculan con los pesos en lugar de una constante 1 / n.
Existen distintas técnicas de desagrupamiento; polígonos, vecino más cercano, celdas. Donde esta última es la comúnmente usada en minería (Journel 1983, Deutsch 1989).
El desagrupamiento mediante celdas funciona de la siguiente manera:
1. Se divide el volumen de interés en una cuadricula de celdas l = 1, …, L.
2. Se cuentan las celdas “Lo” ocupadas y la cantidad de datos en cada celda ocupada “nLo”, Lo = 1, …, Lo.
3. Se pondera cada dato de acuerdo con la cantidad de datos que caen en la misma celda, por ejemplo, para el dato “i” que cae en la celda “l”, el peso de la célula que se desprende es:
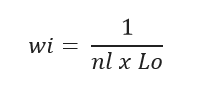
Los ponderadores son mayores que cero y suman uno. A cada celda ocupada se le asigna una ponderación. Una celda desocupada simplemente no recibe ninguna ponderación.
La Figura N° 1, ilustra el procedimiento de desagrupamiento de celdas. El área de interés se divide en una cuadrícula de L = 36 celdas, con Lo = 33 celdas ocupadas. La cantidad de datos en cada celda ocupada se establece moviendo arbitrariamente los datos en los límites de la cuadrícula hacia la derecha y hacia abajo.
Los pesos dependen del tamaño de la celda y el origen de grilla. Es importante tener en cuenta que el tamaño de celda para el desagrupamiento no es el tamaño de celda para el modelado geológico de bloques; simplemente en el primer caso se define una rejilla intermedia que permite asignar un ponderador que se desagrupa.
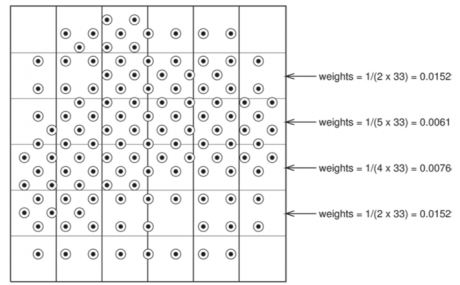
Figura N° 1: Ilustración del método de desagrupamiento mediante celdas
Fuente: Mario E. Rossi, Clayton V. Deutsch., 2014. “Mineral Resource Estimation”. Springer, p. 20.
Cuando el tamaño de la celda es muy pequeña, cada dato está en su propia celda y recibe el mismo peso. Cuando el tamaño de la celda es muy grande, todos los datos caen en una celda y se ponderan por igual.
Elegir el origen de cuadrícula óptimo, la forma de la celda y el tamaño, requiere algunos estudios de sensibilidad. Es común elegir el tamaño de celda para que haya aproximadamente un dato por celda en las áreas escasamente muestreadas o, si está disponible, para elegir de acuerdo a una grilla de muestreo subyacente, casi homogéneo.
Se debe verificar la sensibilidad de los resultados a pequeños cambios en el tamaño de la celda, si los resultados cambian por una gran cantidad, entonces lo más probable es que los pesos estén privilegiando valores extremos (bajos o altos). Como generalmente se sabe si el sobre muestreo ocurre en áreas de alto o bajo valor, las ponderaciones se pueden seleccionar de manera que proporcionen la media mínima o máxima de los datos desagrupados.
Se debe trazar la media desagrupada versus un rango de tamaños de celda, y se debe elegir el tamaño con el valor más bajo (Figura N° 2). Se debe tener cuidado de no sobrepasar el mínimo.
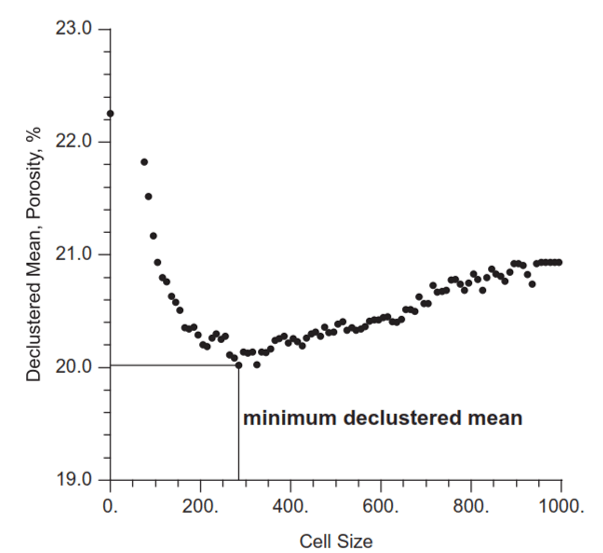
Figura N° 2: Grafico de media desagrupada versus tamaño de celda
Fuente: Mario E. Rossi, Clayton V. Deutsch., 2014. “Mineral Resource Estimation”. Springer, p. 20.
El tamaño de celda correcto debe ser aproximadamente el espaciado de los datos en áreas escasamente muestreadas. Esta verificación cualitativa se puede utilizar para garantizar que no se elija un tamaño de celda demasiado grande o demasiado pequeño.
La forma de las celdas depende de la configuración geométrica de los datos, ya que se ajusta a las direcciones principales del muestreo preferencial. Por ejemplo, si las muestras son más estrechamente espaciados en la dirección X que en la dirección Y, se debe reducir el tamaño de la celda en la dirección X.
El origen de la cuadrícula de datos desagrupado y el número de celdas “L” deben elegirse de modo que todos los datos estén incluidos dentro de la misma. Arreglar el tamaño de la celda y cambiar el origen a menudo conduce a diferentes ponderadores.
Para evaluar este proceso, se utilizan varias ubicaciones de origen de la cuadricula para el mismo tamaño de celda.
A continuación, se promedian las ponderaciones de desagrupamiento para cada desplazamiento en el origen. Se busca el barrido completo en todo el rango de la distribución real. Si este no es el caso, entonces los resultados son parciales y pueden requerirse técnicas de desvinculación de datos.
Ejemplo: Desagrupamiento mediante método de las celdas [Cell Declustering]


Debe estar conectado para enviar un comentario.