EL ABANICO VARIOGRÁFICO
EJEMPLOS USANDO DATAMINE SUPERVISOR
Escrito por Heber Hernández G. (Junio, 2021)
Contenidos
En este breve articulo hablaremos sobre el abanico variográfico, una herramienta geoestadística sumamente útil a la hora de definir las direcciones en las que se modelará la variabilidad espacial para una determinada variable de interés. Su uso es amplio y conocido para geólogos e ingenieros de mina dedicados a la modelización de recursos minerales, y como indica su nombre, es una herramienta basada en el variograma.
¿QUÉ ES EL ABANICO VARIOGRÁFICO?
Es una herramienta geoestadística la cual presenta visualmente y en forma de abanico, la semivarianza de una variable a distintas direcciones del espacio en forma simultánea.
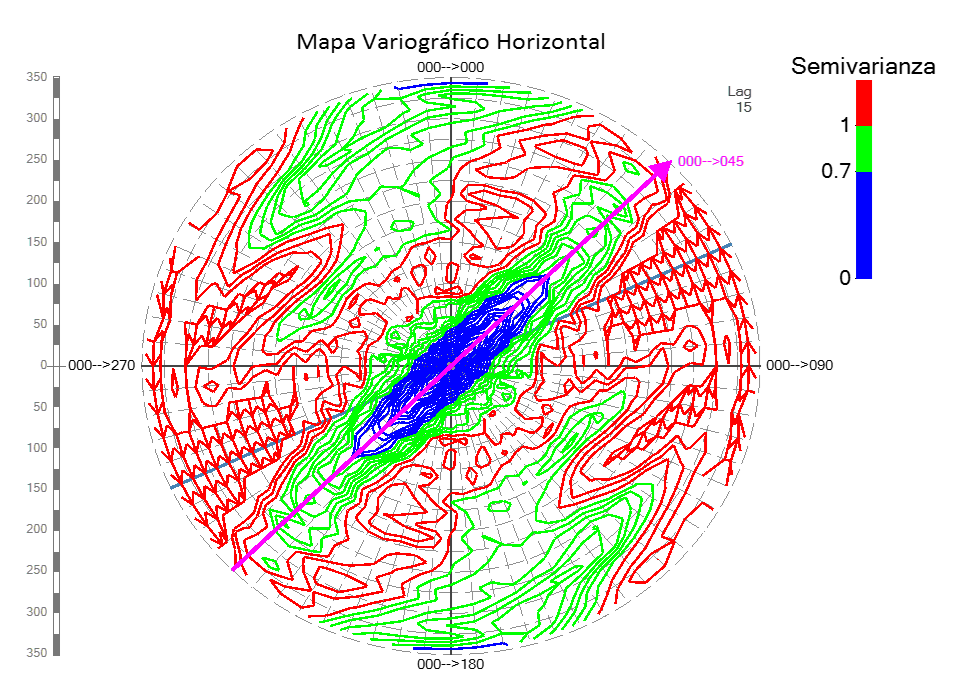
Figura 1. Ejemplo abanico variográfico
El abanico es 2D, y si bien podría indicar cualquier plano en el espacio, el horizontal es el más útil en minería para definir una dirección de anisotropía. Es importante señalar que se miden acimultamente las direcciones en sentido de las manecillas del reloj, donde en la parte superior central está el norte (0°). En el centro del abanico se encuentra el punto de partida de cada dirección, es decir la distancia 0, y a través de una escala gráfica es que se da una idea de la variabilidad a distintos alcances.
¿QUÉ ES LA SEMIVARIANZA?
Recordemos que la semivarianza es una función de correlación espacial que mide la discrepancia de una variable en base al desplazamiento de esta en el espacio. En la práctica se expresa como:
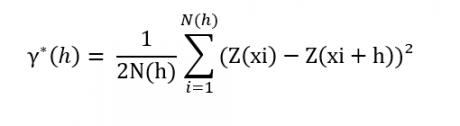
Donde:
– γi(h): Semivarianza
– Zi(x): variable “Z” en ubicación “i”.
– Zi(x+h): variable “Z” en ubicación “i + h”, donde “h” es un vector.
– N(h): Número de pares de datos tomados al vector h.
¿CÚAL ES LA UTILIDAD DEL ABANICO VARIOGRÁFICO?
Nos ayuda a conocer de manera temprana la variabilidad espacial sobre una variable de interés, o puesto de otra forma, nos ayuda a detectar la dirección de anisotropía.
¿QUÉ ES LA ANISOTROPÍA?
El termino anisotropía en análisis espacial, indica la existencia de una dirección de mayor continuidad con respecto al resto de direcciones para una variable.
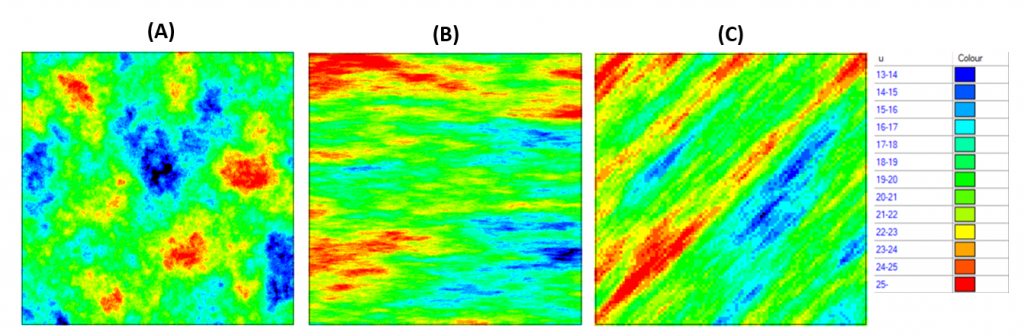
Figura 2. Ejemplo de anisotropía (B y C) e isotropía (A)
Por ejemplo, en la figura 2 podemos ver que en el caso (B) la variable u es mas continua en la dirección horizontal (90° azimut), lo mismo que en (C), donde u es más continua, pero en una dirección diagonal (45° azimut). En estos dos casos hablamos de anisotropía, mientras que para el caso (A), no se distingue una dirección preferente, lo cual señala isotropía, que significa que en todas las direcciones la variable tiene un comportamiento similar.
En estos casos es fácil distinguir si existe o no anisotropía, ya que se trata de escenarios bastante densos en información y solo es un plano (2D), pero recordar que esto ha de ser detectado en una muestra y muchas veces con muy pocos datos como se muestra en la figura 3.
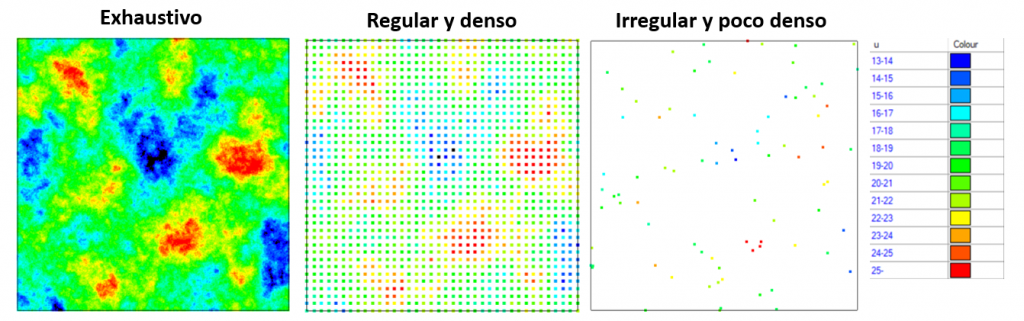
Figura 3. Ejemplo de muestreo regular denso e irregular poco denso
¿CÓMO SE DEBERÍA LEER UN ABANICO VARIOGRÁFICO?
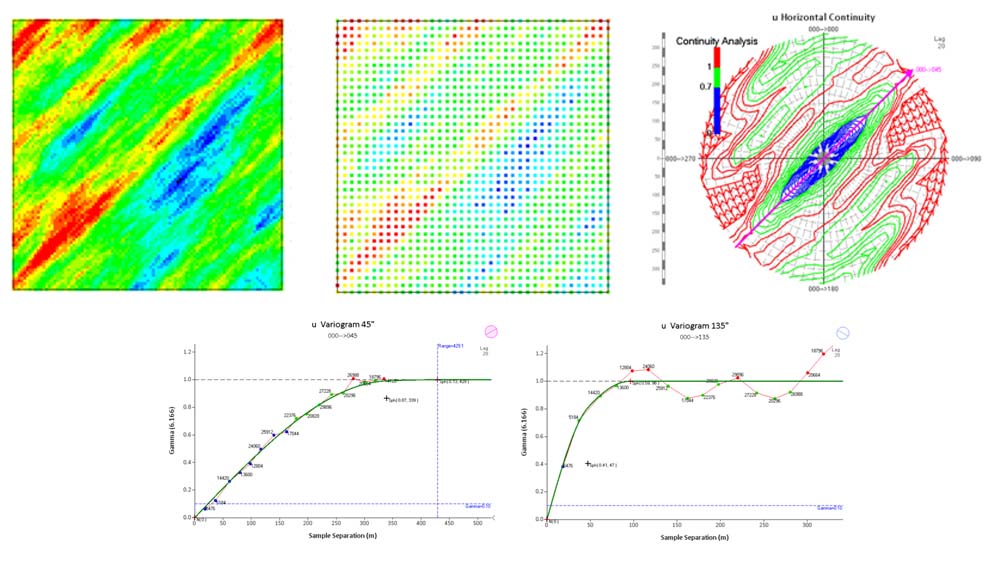
Vamos a tomar el caso C donde existe anisotropía y para el ejemplo, trabajaremos sobre una muestra regular y densa.
Figura 5. Ejemplo anisotropía geométrica
El abanico variografico posee 3 colores; azul para un rango de semivarianza baja que va entre 0 y 0.7, verde para el rango 0.7 a 1 y roja para los valores sobre 1. Ha de saber que la variable u para este ejemplo fue estandarizada (media 0, varianza 1), y es por ello que los puntos que se encuentran por debajo del 70% de la meseta, serán considerados como indicadores de mayor dependencia espacial. El abanico variográfico señala claramente que en la dirección 45° azimut existe una mayor continuidad (alcance de 400 m), y esta se define como dirección de anisotropía. Luego la dirección perpendicular a la de anisotropía, es de 135° azimut, la que como se observa en el variograma, tiene un alcance mucho mas corto (100 m). El tipo de anisotropía que se modela es geométrico, es decir ambas direcciones comparten meseta, pero no así alcances.
Si comparamos el caso C con el A (ver figura 2), es que se aprecia el cambio en la forma que toma el abanico variográfico desde el centro, lo cual indica que en todas las direcciones la dependencia es similar (alcances similares).
Figura 5. Ejemplo isotropía caso A
¿DÓNDE ENCONTRAR ESTA HERRAMIENTA?
De forma gratuita y desde 1998 se puede encontrar en la GSLIB (Geostatistical Software Library), bajo el nombre de VARMAP. También su reimplementación en Python a través de la biblioteca GeostatsPy. La limitación de estas opciones es que trabaja sobre un único entorno 2D y ha de tener nociones de programación normalmente para controlar las variables e imprimir los resultados. Ya en software comercial para minería, es que se encuentra en la mayoría de aquellos dedicados a la caracterización de recursos minerales. En estos últimos se hace mucho más simple y rápido el obtener los resultados, así igual existen controles adicionales que facilitan la construcción e interpretación de los abanicos.
¿CÓMO REALIZAR UN ABANICO VARIOGRÁFICO EN DATAMINE SUPERVISOR?
En el video a continuación se muestra la construcción de un abanico variográfico sobre un caso 2D y 3D.
REFERENCIAS
Deutsch, Clayton (2002). Geostatistical Reservoir Modeling.
Geoestatistical Software Library (2000). GSLIB source code and DOS executable [online]. Disponible en <http://www.statios.com/Quick/gslib.html> [14 de junio 2021].