OPTIMIZACIÓN DE PIT MEDIANTE MÉTODO DE FLUJO MÁXIMO
El problema inicial de la minería a cielo abierto es determinar la envolvente económica optima, de modo que se maximice el valor presente neto (VPN) de la operación minera.
En su artículo de 1965, Lerchs y Grossmann indicaron que el problema del pit final podría expresarse como un problema de flujo de red de cierre máximo, pero recomendaron su enfoque directo, posiblemente debido a las limitaciones de memoria de la computadora en ese momento. Por lo tanto, el algoritmo LG fue un método para resolver un caso especial de un problema de flujo de red. (Deutsch, et al, 2015).
En 1976, Picard “proporcionó una prueba matemática de que un problema de flujo de red de “cierre máximo” (de los cuales el problema de optimización de pit es uno) era reducible a un problema de flujo de red de “corte mínimo”, por lo tanto, solucionable por cualquier algoritmo de flujo máximo eficiente. Como consecuencia, se podrían usar sofisticados algoritmos de flujo de red en lugar del algoritmo LG, y se pueden calcular resultados idénticos en una fracción de tiempo”. (Deutsch, et al, 2015).
Los métodos de flujo máximo se utilizan para determinar la cantidad máxima de material que se puede extraer de la mina en un período de tiempo determinado. Este método utiliza un modelo de red que representa la mina y los caminos por los que se transporta el material. La red se compone de nodos y arcos, donde los nodos representan los lugares donde se encuentra el mineral/ estéril y los arcos representan los caminos que conectan los nodos entre sí y con sus respectiva fuente de mineral y destino de estéril.
Ejemplo
1. Partamos con una matriz de 2 filas y 4 columnas, con un total de 8 bloques representados desde “a”, hasta “h”. Este será nuestra reducción de un modelo de bloques (corte vertical en sección).
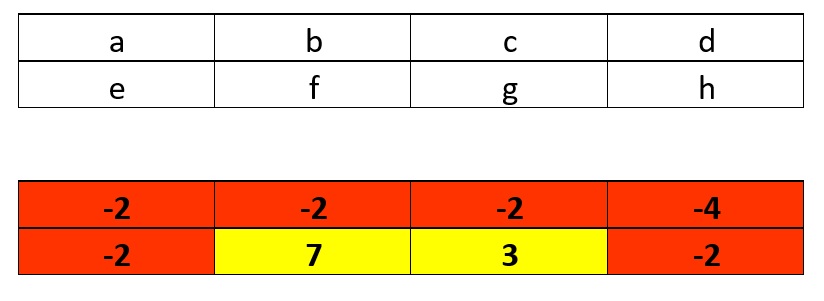
2. Cada bloque tiene un valor neto asociado, en algunos casos positivos como es el caso de “f” y “g” y otros negativos (todo el resto).
3. Asumiremos una restricción geotécnica para la extracción de bloques con un ángulo de 45 grados. Por ejemplo, para extraer “g” debe primero extraerse “b”, “c” y “d”.
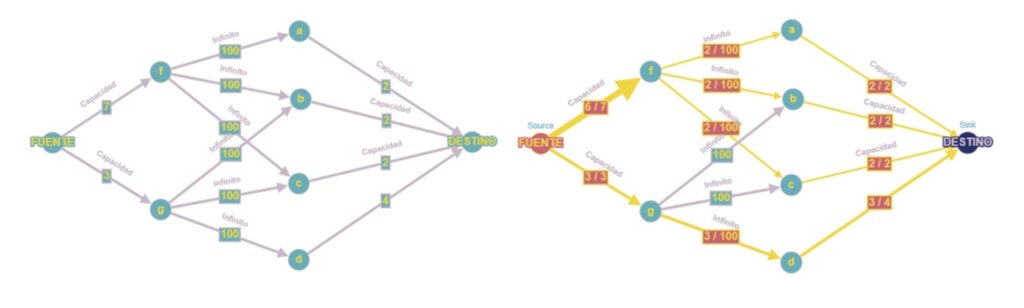
4. El modelo de bloques debe convertirse en una red de flujo, cada bloque en un nodo, los arcos dados por la restricción de ángulo de talud y cada valor neto en una capacidad de arco. Estas capacidades serán expresadas en valor absoluto. El nodo artificial “FUENTE” será conectado con los nodos de mineral, mientras que el “DESTINO” con el estéril. Estas conexiones serán los arcos externos, mientras que los arcos internos tendrán capacidades infinitas (en el ejemplo figurará con valor 100 solo por cuestiones de uso del algoritmo disponible en https://graphonline.ru/).
5. Desde ahora se podrá usar cualquier método de flujo máximo para optimizar la red (Ford-Fulkerson, Push-Re-Label, Pseudoflow, etc), lo que buscamos es conocer los flujos óptimos que pasen por cada arco para posteriormente cortar los arcos saturados y delimitar el pit final.
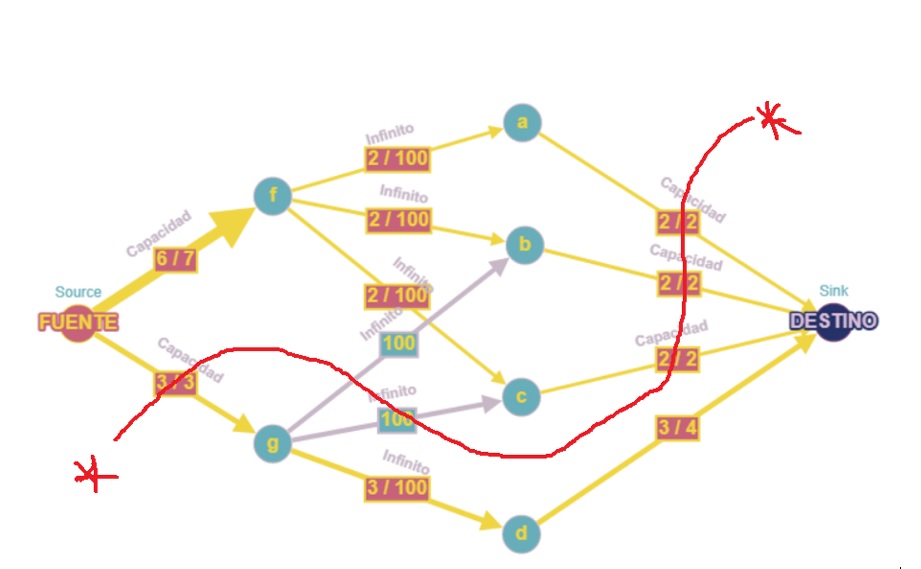
6. Seleccionando los nodos “f”, “a”, “b” y “c” se resuelve el problema de pit final, obteniendo un beneficio total de 1.
De esta manera muy resumida, es como se lleva a cabo la optimización de pit a través de métodos de flujo máximo y corte mínimo. Si es de vuestro interés profundizar en estos métodos y entender con ejemplos paso a paso, sobre todo el punto 5 de métodos de flujo máximo, es que recomiendo puedas ver el contenido del curso: OPTIMIZACIÓN DE MINAS A CIELO ABIERTO CON MÉTODOS DE FLUJO MÁXIMO.