Ley de Corte - Método de Kenneth Lane
LUIS ÁLVAREZ P.
(11 de Septiembre, 2024)
Tabla de contenidos
Sobre el método
El método conocido como K-LANE, es utilizado para determinar la ley de corte óptima en operaciones mineras, ya sea a cielo abierto o subterráneas.
El método considera varios factores, como los costos de extracción, procesamiento, transporte y venta del mineral, así como las leyes minerales y los precios de mercado del producto de interés. La clave del método es su capacidad para optimizar dinámicamente la ley de corte en función de cambios en estos parámetros, permitiendo así una gestión más eficiente y rentable del recurso mineral.
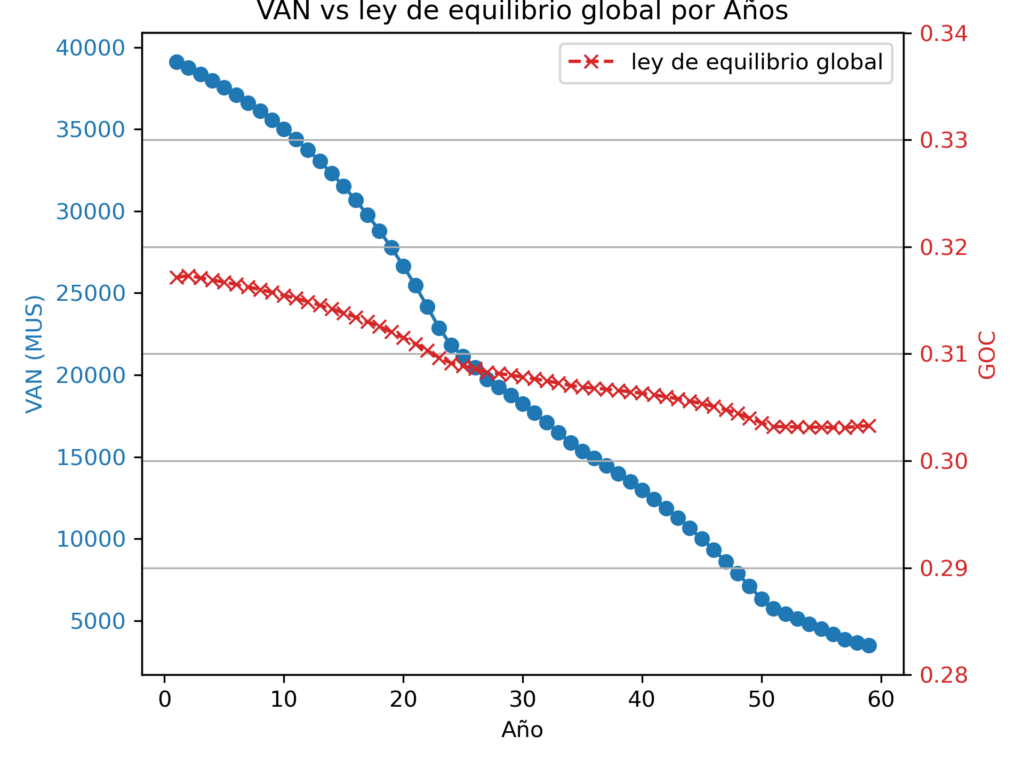
En términos generales, el objetivo es maximizar el valor presente neto (VPN) de la operación minera. Para ello, el método evalúa las diferentes leyes de corte posibles y selecciona aquella que genere el mayor rendimiento económico posible, considerando no solo el valor del mineral recuperado, sino también los costos asociados y las limitaciones operativas de la mina.
El método K-LANE también se adapta a diferentes escenarios y puede incorporar factores adicionales como los impactos ambientales, el uso de tecnologías de preconcentración, y las incertidumbres en los precios de los metales. Por ejemplo, algunos estudios han propuesto modificaciones al método original para incluir costos ambientales o utilizar algoritmos de optimización metaheurística para mejorar aún más la precisión del punto de equilibrio económico.
En resumen, el método es una herramienta robusta y flexible para la optimización de la ley de corte en operaciones mineras, permitiendo una gestión más estratégica y eficiente del recurso, con el objetivo de maximizar el retorno económico de la explotación minera.
Ejemplo implementado en Python
Este es un ejemplo desarrollado paso a paso para la implementación del método de K-LANE. Y por supuesto es reutilizable en cualquier inventario de recursos siempre y cuando este mantenga el mismo formato del de nuestro ejemplo.
I = [0, 0.2, 0.4, 0.6, 0.8, 1, 1.2, 1.4, 1.6, 1.8, 2.0, 2.2]
S = [0.2, 0.4, 0.6, 0.8, 1, 1.2, 1.4, 1.6, 1.8, 2.0, 2.2, 2.4]
TP = [350, 530, 620, 725, 525, 460, 470, 320, 220, 250, 220, 210]
# Crear DataFrame
invrecursos = {'Inferior': I, 'Superior': S, 'Ton Parcial': TP}
df = pd.DataFrame(invrecursos)
# Parámetros económicos y operacionales
s = 3.5 # Precio (Us/lb)
r = 0.2 # Costos de venta refineria y transporte (Us/lb)
c = 15 # Costo Mina (Us/ton)
m = 2.0 # Costo Planta (Us/ton)
f = 6.5 # Costo fijo anual (M)
R = 1.1 # Recuperación (Mt)
C = 100 # Tasa de producción de planta (Mt)
M = 200.0 # Tasa de producción de Mina (Mt)
i = 0.1 # Tasa de descuento (%)
y = 0.7 # Recuperación metalúrgica
Parámetros del método
años = 60 # cantidad de años a evaluar el VAN
itera= 3 # cantidad de iteraciones del VAN por cada año
# nota: si sale un error al finalizar es posible que tengas una
#cantidad de años que supera el recurso disponible, es bueno ver en
# los resultados, el ultimo año con resultados para ir ajustado
# Lista para almacenar los valores de VAN en cada iteración
valores_VAN = []
valores_GOC = []
# Inicialización de la variable para el cálculo del inventario
Qmc_anual_anterior = 0
# Inicialización de la variable para la iteración
nuevo_B_anual_anterior = 0
# Definir la función para calcular el nuevo beneficio anual
def calcular_nuevo_beneficio_anual(B_anual, Qmc_anual, Qcc_anual, Qrc_anual, i, T):
nuevo_B_anual = (2204.6 * (s - r) * Qrc_anual * 1000000 - m * Qmc_anual * 1000000 - c * Qcc_anual * 1000000 - f * 1000000) / 1000000
VAN = nuevo_B_anual * ((((1 + i) ** T) - 1) / (((1 + i) ** T) * i))
return nuevo_B_anual, VAN
# Iterar para cada año
for year in range(1, años):
print(f"Año {year}:")
# Calcular Qmc_anual para el año actual
Qmc_anual = Qmc_anual_anterior if year > 1 else 0
# Actualizar el inventario para el año actual
df['Ton Parcial'] -= Qmc_anual / len(df)
# Asegurarnos de que los valores no sean negativos
df['Ton Parcial'] = df['Ton Parcial'].clip(lower=0)
# Crear DataFrame
df_original = df.copy() # Crear una copia del DataFrame original
# Crear la columna 'Xi' que es el promedio entre 'Inferior' y 'Superior'
df['Xi'] = (df['Inferior'] + df['Superior']) / 2
# Calcular el tonelaje acumulado desde abajo hacia arriba
df['ton_acum'] = df['Ton Parcial'][::-1].cumsum()[::-1]
# Crear la columna 'Fino' que es la multiplicación de 'Xi' por 'Ton Parcial' dividido entre 100
df['Fino'] = (df['Xi'] * df['Ton Parcial']) / 100
# Calcular el fino acumulado desde abajo hacia arriba
df['fino_acum'] = df['Fino'][::-1].cumsum()[::-1]
# Calcular la Ley Media Ponderada
df['LeyMedia'] = (df['fino_acum'] / df['ton_acum']) * 100
# Calcular el tonelaje total
ton_total = df['Ton Parcial'].sum()
# Crear la columna 'Qm' que es el tonelaje acumulado dividido en el tonelaje total, multiplicado por 100
df['Qm'] = ton_total
# Crear la columna 'Qc' que es el tonelaje acumulado dividido en el tonelaje total, multiplicado por 100
df['Qc'] = (df['ton_acum'] / ton_total) * 100
# Crear la columna 'Qr' que es el fino acumulado
df['Qr'] = ton_total * df['Qc'] / 100 * df['LeyMedia'] / 100 * y
# Crear la columna 'Qr2' que es el fino acumulado
df['Qr2'] = C * df['LeyMedia'] * (y / 100)
print(df)
# Iterar para cada iteración dentro del año
for iteracion in range(1, itera):
print(f"Iteración {iteracion}:")
###opcion que cada año comience con B de la ultima iteracion
#Inicialización de variables para el primer año
if iteracion == 1 and year == 1:
B_anual_actual = 0
else:
#Usar el beneficio anual obtenido en la última iteración del año anterior como B_anual inicial
B_anual_actual = nuevo_B_anual_anterior
###opcion que cada año comience con B=0
#if iteracion == 1:
# # En la primera iteración de cada año, establecer B_anual_actual en 0
# B_anual_actual = 0
#else:
# # En las iteraciones posteriores dentro del mismo año, utilizar el beneficio anual calculado en la iteración anterior
# B_anual_actual = nuevo_B_anual_anterior
# Imprimir el beneficio anual actual
print(f"B_anual_actual en Iteración {iteracion}, Año {year}: {B_anual_actual}")
Procedimiento en 12 pasos
# 1 PASO
# Ley de Corte Mina (gm)
gm = (c / (2204.6 * (s - r) * y)) * 100
# Ley de Corte Planta (gc)
gc = ((c + ((f + (i * B_anual_actual)) / C)) / (2204.6 * (s - r) * y)) * 100
# Ley de Corte Refineria (gr)
gr = (c / (2204.6 * (s - r) * y - ((f + (i * B_anual_actual)) / R))) * 100
# 2 PASO
# Calculando las razones de capacidad
# Capacidad de la mina (Qm)
Q_m = M
# Capacidad de la planta (Qc)
Q_c = C
# Capacidad de la refinería (Qr)
Q_r = R # Debido a que la refinería procesa la producción de la mina
# Razón de capacidad entre la mina y la planta (Qc/Qm)
ratio_mina_planta = Q_c / Q_m
# Razón de capacidad entre la mina y la refinería (Qr/Qm)
ratio_mina_ref = Q_r / Q_m
# Razón de capacidad entre la planta y la refinería (Qr/Qc)
ratio_planta_ref = Q_r / Q_c
# 3 PASO
#ley de equilibrio mina-planta gmc
Q_c = C # Capacidad de la planta (Qc)
def get_inferior_for_Qc(Q_c):
# Verificar si el valor de Q_c está exactamente en la columna 'Qc'
if Q_c in df['Qc'].values:
# Si el valor de Q_c está exactamente en la columna 'Qc', devolvemos el valor de 'Inferior'
return df.loc[df['Qc'] == Q_c, 'Inferior'].iloc[0]
else:
# Encontrar los valores más cercanos tanto por debajo como por encima de Q_c en la columna Qc
lower_row = df[df['Qc'] > Q_c].iloc[-1] if (df['Qc'] > Q_c).any() else None
upper_row = df[df['Qc'] < Q_c].iloc[0] if (df['Qc'] < Q_c).any() else None
if lower_row is None:
return upper_row['Inferior']
elif upper_row is None:
return lower_row['Inferior']
else:
# Realizar interpolación lineal entre las filas
inferior_lower = lower_row['Inferior']
inferior_upper = upper_row['Inferior']
Qc_lower = lower_row['Qc']
Qc_upper = upper_row['Qc']
# Interpolación lineal
inferior = inferior_lower + (Q_c - Qc_lower) * (inferior_upper - inferior_lower) / (Qc_upper - Qc_lower)
return inferior
# Utilizar la función para obtener el valor de 'Inferior' para un valor de Q_c dado
inferior_value = get_inferior_for_Qc(Q_c)
gmc = inferior_value
####### Ley de equilibrio Mina-Refineria (gmr) ###############
Q_r = R # Capacidad de la refineria (Qr)
def get_inferior_for_Qr(Q_r):
# Verificar si el valor de Q_r está exactamente en la columna 'Qr'
if Q_r in df['Qr'].values:
# Si el valor de Q_r está exactamente en la columna 'Qr', devolvemos el valor de 'Inferior'
return df.loc[df['Qr'] == Q_r, 'Inferior'].iloc[0]
else:
# Encontrar los valores más cercanos tanto por debajo como por encima de Q_r en la columna Qr
lower_row_r = df[df['Qr'] > Q_r].iloc[-1] if (df['Qr'] > Q_r).any() else None
upper_row_r = df[df['Qr'] < Q_r].iloc[0] if (df['Qr'] < Q_r).any() else None
if lower_row_r is None:
return upper_row_r['Inferior']
elif upper_row_r is None:
return lower_row_r['Inferior']
else:
# Realizar interpolación lineal entre las filas
inferior_lower_r = lower_row_r['Inferior']
inferior_upper_r = upper_row_r['Inferior']
Qr_lower = lower_row_r['Qr']
Qr_upper = upper_row_r['Qr']
# Interpolación lineal
inferior_r = inferior_lower_r + (Q_r - Qr_lower) * (inferior_upper_r - inferior_lower_r) / (Qr_upper - Qr_lower)
return inferior_r
# Utilizar la función para obtener el valor de 'Inferior' para un valor de Q_c dado
inferior_value_r = get_inferior_for_Qr(Q_r)
gmr = inferior_value_r
####### Ley de equilibrio Planta-Refineria (gcr) ###############
Q_r = R # Capacidad de la refineria (Qr2)
def get_inferior_for_Qr2(Q_r):
# Verificar si el valor de Q_r está exactamente en la columna 'Qr2'
if Q_r in df['Qr2'].values:
# Si el valor de Q_r está exactamente en la columna 'Qr2', devolvemos el valor de 'Inferior'
return df.loc[df['Qr2'] == Q_r, 'Inferior'].iloc[0]
else:
# Encontrar los valores más cercanos tanto por debajo como por encima de Q_r en la columna Qr2
lower_row_r2 = df[df['Qr2'] < Q_r].iloc[-1] if (df['Qr2'] < Q_r).any() else None
upper_row_r2 = df[df['Qr2'] > Q_r].iloc[0] if (df['Qr2'] > Q_r).any() else None
if lower_row_r2 is None:
return upper_row_r2['Inferior']
elif upper_row_r2 is None:
return lower_row_r2['Inferior']
else:
# Realizar interpolación lineal entre las filas
inferior_lower_r2 = lower_row_r2['Inferior']
inferior_upper_r2 = upper_row_r2['Inferior']
Qr2_lower = lower_row_r2['Qr2']
Qr2_upper = upper_row_r2['Qr2']
# Interpolación lineal
inferior_r2 = inferior_lower_r2 + (Q_r - Qr2_lower) * (inferior_upper_r2 - inferior_lower_r2) / (Qr2_upper - Qr2_lower)
return inferior_r2
# Utilizar la función para obtener el valor de 'Inferior' para un valor de Q_r dado
inferior_value_r2 = get_inferior_for_Qr2(Q_r)
gcr = inferior_value_r2
# 4 PASO
#### Determinar Gmc #######
# Ordenar los valores
sorted_values_mc = sorted([gm, gc, gmc])
# Determinar el valor medio
G_mc = sorted_values_mc[1]
#### Determinar Gmr #######
# Ordenar los valores
sorted_values_mr = sorted([gm, gr, gmr])
# Determinar el valor medio
G_mr = sorted_values_mr[1]
#### Determinar Gcr #######
# Ordenar los valores
sorted_values_cr = sorted([gc, gr, gcr])
# Determinar el valor medio
G_cr = sorted_values_cr[1]
# 5 PASO: ley de equilibrio global GOC
#### Determinar GOC #######
# Ordenar los valores
sorted_values_GOC = sorted([G_mc, G_mr, G_cr])
# Determinar el valor medio
GOC = sorted_values_GOC[1]
print('La ley GOC es:', GOC)
# 6 PASO: Ley Media asociada a GOC
# Encontrar el valor de 'Inferior' asociado a GOC
def get_Inferior_for_Inferior(GOC):
# Verificar si el valor de GOC está exactamente en la columna 'Inferior'
if GOC in df['Inferior'].values:
# Si el valor de GOC está exactamente en la columna 'inferior', devolvemos el valor de 'LeyMedia'
return df.loc[df['Inferior'] == GOC, 'LeyMedia'].iloc[0]
else:
# Encontrar los valores más cercanos tanto por debajo como por encima de GOC en la columna Ley_Media
lower_row_GOC = df[df['Inferior'] < GOC].iloc[-1] if (df['Inferior'] < GOC).any() else None
upper_row_GOC = df[df['Inferior'] > GOC].iloc[0] if (df['Inferior'] > GOC).any() else None
if lower_row_GOC is None:
return upper_row_GOC['LeyMedia']
elif upper_row_GOC is None:
return lower_row_GOC['LeyMedia']
else:
# Realizar interpolación lineal entre las filas
inferior_lower_GOC = lower_row_GOC['LeyMedia']
inferior_upper_GOC = upper_row_GOC['LeyMedia']
Ley_Media_lower = lower_row_GOC['Inferior']
Ley_Media_upper = upper_row_GOC['Inferior']
# Interpolación lineal
inferior_GOC = inferior_lower_GOC + (GOC - Ley_Media_lower) * (inferior_upper_GOC - inferior_lower_GOC) / (Ley_Media_upper - Ley_Media_lower)
return inferior_GOC
# Utilizar la función para obtener el valor de 'Inferior' para GOC
inferior_value_GOC = get_Inferior_for_Inferior(GOC)
print("La ley Media de GOC es:", inferior_value_GOC)
Lm_GOC=inferior_value_GOC
# 7 PASO: Tonelaje acumulado asociada a GOC
def get_ton_acum_for_inferior(GOC):
# Verificar si el valor de GOC está exactamente en la columna 'inferior'
if GOC in df['Inferior'].values:
# Si el valor de GOC está exactamente en la columna 'Inferior', devolvemos el valor de 'Inferior'
return df.loc[df['Inferior'] == GOC, 'ton_acum'].iloc[0]
else:
# Encontrar los valores más cercanos tanto por debajo como por encima de Q_r en la columna Qr2
lower_row_t = df[df['Inferior'] < GOC].iloc[-1] if (df['Inferior'] < GOC).any() else None
upper_row_t = df[df['Inferior'] > GOC].iloc[0] if (df['Inferior'] > GOC).any() else None
if lower_row_t is None:
return upper_row_t['ton_acum']
elif upper_row_t is None:
return lower_row_t['ton_acum']
else:
# Realizar interpolación lineal entre las filas
ton_acum_lower_t = lower_row_t['ton_acum']
ton_acum_upper_t = upper_row_t['ton_acum']
inferior_lower_t = lower_row_t['Inferior']
inferior_upper_t = upper_row_t['Inferior']
# Interpolación lineal
inferior_t = ton_acum_lower_t + (GOC - inferior_lower_t) * (ton_acum_upper_t - ton_acum_lower_t) / (inferior_upper_t - inferior_lower_t)
return inferior_t
# Utilizar la función para obtener el valor de 'Inferior' para un valor de Q_r dado
inferior_value_GOCT = get_ton_acum_for_inferior(GOC)
print("El Tonelaje de GOC:", inferior_value_GOCT)
Ton_GOC = inferior_value_GOCT
# 8 PASO: Moviemiento de material asociado a GOC
#ton_total = df['Ton Parcial'].sum()
Qmc = ton_total
print("El Qm+c de GOC es:", Qmc)
Qcc = Ton_GOC
print("El Qc+c de GOC es:", Qcc)
Qrc = Qcc*(Lm_GOC/100)*y
print("El Qr+c de GOC es:", Qrc)
# 9 PASO Periodo de operación
P_mina = ton_total/M
print("El Periodo Mina asociado a Qm+c es:", P_mina)
P_planta = Qcc/C
print("El Periodo Planta asociado a Qc+c es:", P_planta)
P_refineria = Qrc/R
print("El Periodo Refineria asociado a Qr+c es:", P_refineria)
# Ordenar los valores
sorted_values_T = sorted([P_mina, P_planta, P_refineria])
# Determinar el valor maximo
T = sorted_values_T[2]
print("El valor de T es:", T)
#10 PASO: Tonelaje sobre GOC Anual
Qmc_anual = Qmc/T
print("El Qm+c_anual de GOC es:", Qmc_anual)
Qcc_anual = Qcc/T
print("El Qc+c_anual de GOC es:", Qcc_anual)
Qrc_anual = Qrc/T
print("El Qr+c_anual de GOC es:", Qrc_anual)
# 11 PASO: Beneficio anual
B_anual = (2204.6*(s - r)*Qrc_anual*1000000 - m*(Qmc_anual)*1000000 - c*(Qcc_anual)*1000000 - f*1000000)/1000000
print("El Beneficio Anual (MUS) es :", B_anual)
# 12 PASO: VAN
VAN = B_anual*( (((1+ i )**T ) -1) / (((1+ i)**T)*(i)))
print("El VAN (MUS) es :", VAN)
# Actualizar el beneficio anual anterior para la próxima iteración
nuevo_B_anual_anterior = B_anual
# Guardar Qmc_anual de la última iteración del año actual
Qmc_anual_anterior = Qmc_anual
# Guardar el VAN de la última iteración del año actual
valores_VAN.append(VAN)
# Agregar el valor de GOC a la lista de valores de GOC
valores_GOC.append(GOC)
# Obtener el máximo valor de GOC
max_GOC = max(valores_GOC)
# Definir el límite del eje y del segundo eje
ylim_max = 0.34
ylim_min = 0.28
# Generar el gráfico de VAN versus años
fig, ax1 = plt.subplots()
color = 'tab:blue'
ax1.set_xlabel('Año')
ax1.set_ylabel('VAN (MUS)', color=color)
ax1.plot(range(1, len(valores_VAN) + 1), valores_VAN, marker='o', label='VAN', color=color)
ax1.tick_params(axis='y', labelcolor=color)
ax2 = ax1.twinx()
color = 'tab:red'
ax2.set_ylabel('GOC', color=color)
ax2.plot(range(1, len(valores_GOC) + 1), valores_GOC, marker='x', linestyle='--', color=color, label='GOC')
ax2.tick_params(axis='y', labelcolor=color)
# Configurar el límite del eje y del segundo eje
ax2.set_ylim([ylim_min, ylim_max])
fig.tight_layout()
plt.title('VAN vs GOC por Años')
plt.legend()
plt.grid(True)
plt.show()
Resultados
Compartir en facebook
Facebook
Compartir en twitter
Twitter
Compartir en linkedin
LinkedIn
Compartir en whatsapp
WhatsApp