
El método k nearest neighbors (k-NN), en español k vecinos más cercanos, es un algoritmo de aprendizaje supervisado no paramétrico, basado en un conjunto de datos de entrenamiento, que deriva de los métodos de aprendizaje automático o machine learning.
Básicamente se entrena un algoritmo, alimentándolo de un set de variables de entrada, con su respectiva variable de salida (preguntas y respuesta). Este método es muy popular en la clasificación de variables discretas, y en menor medida en la regresión de funciones con valores continuos (a revisar en este caso).
El que sea un algoritmo supervisado, quiere decir que deduce una función a partir de un conjunto de datos entrenados. Que sea no paramétrico, señala que no está basado en un tipo de distribución en específico (por ejemplo distribución normal o lognormal).
Si vamos a los orígenes, este método es una extensión mejorada de la regla de interpolación multivariable del vecino más cercano, la cual consiste en estimar el valor de un dato desconocido a partir de las características del dato más próximo, según una medida de similitud o distancia, denominada métrica. El utilizar no uno, sino un conjunto k de datos más cercanos para predecir el valor de los nuevos datos, provoca disminuir ruido y suavizar la estimación.
En esta demostración del algoritmo, se utiliza la biblioteca Scikit Learn de Python, trabajando con las variables; Fe, SiO2, Al2O3, contenidas en un dataset sintético bidimensional (figura 1). Es importante señalar que estas variables están contenidas en muestras (instancias).
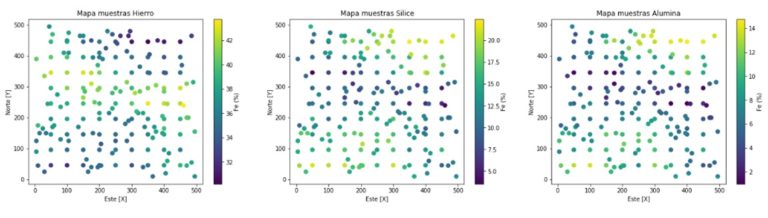
Figura 1. Mapa de muestras Fe, SiO2, Al2O3 en espacio 2D
El objetivo consiste en estimar la concentración de hierro (Fe) a partir de los contaminantes; sílice y alúmina.
Tabla 1. Encabezado dataset sintético
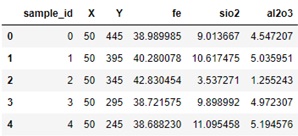
Las dos primeras variables de la tabla 1 corresponden a la ubicación de la muestra en el espacio (no intervienen en el proceso de estimación). La concentración de hierro (Fe), se define como atributo objetivo (variable de salida a estimar), mientras que la sílice y la alúmina son atributos descriptivos (variables de entrada). En otras palabras tenemos una serie de combinaciones finitas entre los atributos descriptivos y objetivo, los cuales se entrenaran para luego estimar la concentración de hierro a partir de combinaciones de contaminantes. Los estadísticos descriptivos de las variables se presentan en la tabla 2., luego la correlación entre las variables descriptivas y objetivo se presentan en la figura 2.
Tabla 2. Estadísticos de posición y dispersión variables

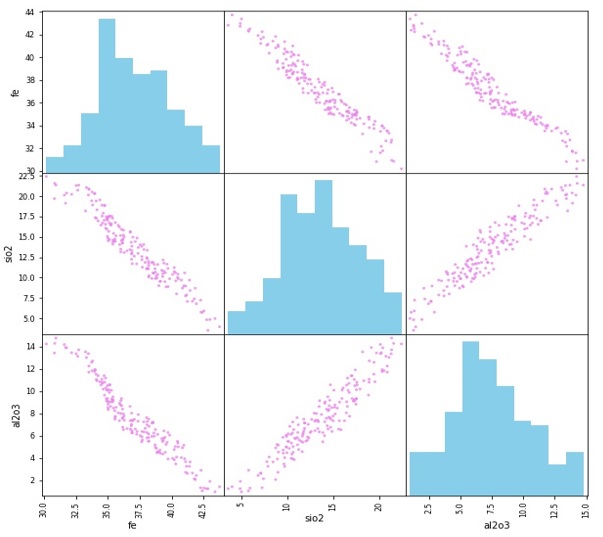
Figura 2. Matriz diagrama de dispersión e histogramas dataset

Una recomendación, es que las variables descriptivas estén normalizadas para evitar que los valores más altos dominen el cálculo de la métrica de similitud.
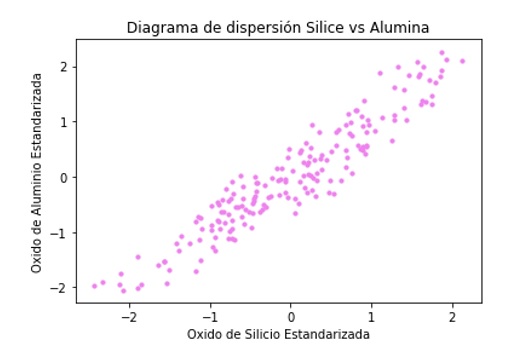
Figura 3. Diagrama de dispersión sílice y alúmina normalizadas

KER es una función Kernel que determina la ponderación de cada punto basado en la distancia al punto de referencia dada por la función D. La función Kernel corresponde al peso que se le da a los datos para obtener un promedio ponderado, por lo tanto debe variar inversamente con la distancia para que los puntos más cercanos tengan mayor peso (mayor importancia). En este ejemplo se utiliza la distancia Minkowski (D) con p=2 que es equivalente a la distancia Euclidea.
Sin duda la etapa de entrenamiento es la más importante. Como los k-NN necesitan la definición a priori del número de vecinos k, este parámetro se selecciona en la etapa de entrenamiento utilizando validación cruzada. La validación cruzada consiste en dividir el bloque de datos de entrenamiento en n partes iguales. Luego para un cierto valor de hiperparámetros, se utilizan n-1 de las n partes para entrenar la herramienta y la parte restante para hallar el error de validación. Este proceso se realiza n veces, lo que permite usar todas las muestras para hallar un error de validación o de desempeño. Por último, se promedian los n valores de error de validación encontrados para obtener un valor asociado al parámetro en uso. Éste procedimiento se repite desde k=1 hasta k=número total de datos, y se escoge el parámetro k que tenga un menor error de validación cruzada. De esta manera, se puede afirmar que el parámetro escogido por validación cruzada es el que tendrá mejor comportamiento ante datos desconocidos.
En este caso de ejemplo, el valor k obtenido es igual a 5.
La cantidad de muestras que se utiliza para el entrenamiento es de 144, equivalente al 80% del total, luego el 20% restante es utilizado para la etapa de “prueba”, posterior validación. La exactitud medida del método en este ejemplo es del 95%.
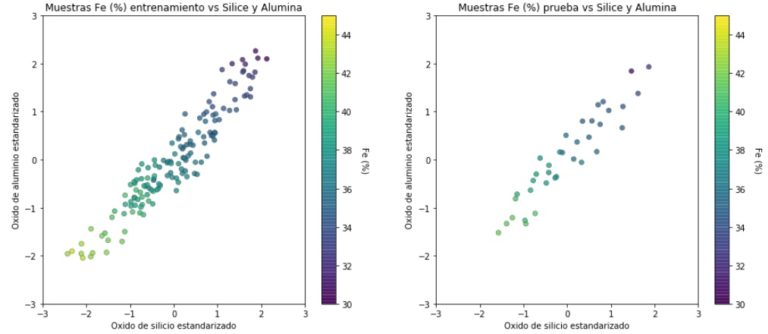
Figura 4. Diagramas estimación variable objetivo en función variables descriptivas
Los resultados de la validación cruzada alcanzan un 98% de coeficiente de correlación lineal.
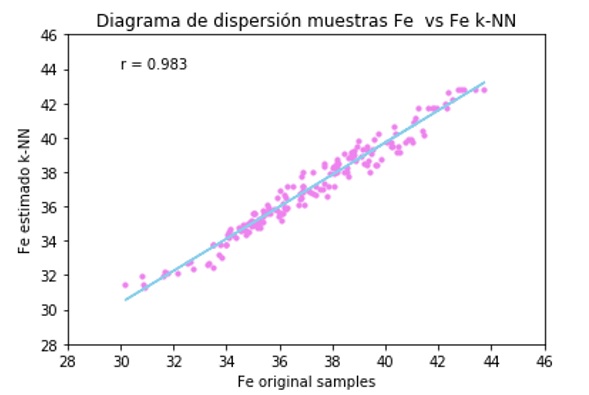
Figura 5. Diagrama de dispersión y ajuste de regresión lineal Fe original vs Fe k-NN
Finalmente podemos representar visualmente el modelo de k-NN como:
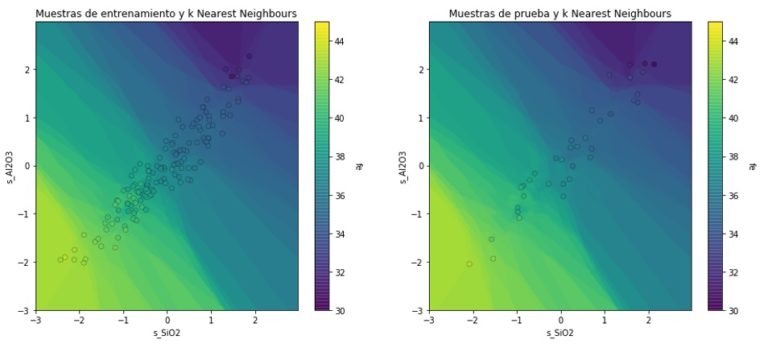
Recursos utilizados:
Lenguaje de programación Python en plataforma Jupyter Notebook.
Bibliotecas Pandas, Numpy, Matplotlib, Scikit Learn.


Debe estar conectado para enviar un comentario.