MODELAMIENTO GEOLÓGICO IMPLÍCITO
METODOLOGÍA DE FUNCIÓN DE DISTANCIA CON SIGNO E INTERPOLADOR CON FUNCIONES DE BASE RADIAL

HERNÁNDEZ H.
(22 de abril de 2022)
Tabla de contenidos

Modelamiento geológico
Un modelo geológico es una representación conceptual de la realidad incierta, pero probable, de diversas unidades geológicas, provenientes de atributos como la litología, alteración, mineralogía, estructuras, y otros fenómenos presentes en el macizo rocoso. Constituye una etapa temprana e indispensable en la estimación de recursos minerales, al ser el punto de conexión entre la geología y la ingeniería.
El punto de partida para la elaboración de un modelo geológico son los sondajes de exploración, estos corresponden a un fragmento (muestra) con la cual se deberá interpretar la extensión, la forma y el volumen de cada unidad. Ha de considerar que el conocimiento sobre el tipo de deposito mineral, su formación y comportamiento espacial del o los fenómenos geológicos, ayudara notablemente en la precisión que tenga el modelo.
En la actualidad existen dos principales enfoques en la modelización geológica; métodos deterministas y estocásticos. En esta ocasión hablare solamente de los primeros, que pueden ser separados en modelos explícitos e implícitos.
Las funciones explicitas son del tipo y = f(x), donde «y», se obtiene directamente a partir de los valores de «x», mientras que en las funciones implícitas se tiene un formato general de f(x,y) = 0. Esta segunda función es bastante conveniente en el modelado geológico, ya que cuando el resultado sea cero, se definirá un punto de separación entre estar dentro de una unidad (<0) o fuera de la misma (>0).
Modelamiento explícito
El modelado explicito requiere la proyección de los sondajes en secciones en serie con la respectiva variable categórica a modelar, para luego unir los límites de las unidades similares mediante polilíneas. Esto se realiza en dos juegos de secciones transversales, para posteriormente unir las intersecciones en un tercer juego de secciones en planta y triangularlo resultando en un solido posible de cubicar.
Algunas desventajas de este tipo de modelado es que consume mucho tiempo al ser un proceso completamente manual, además de requerir de un geólogo modelador experimentado para construir geometrías complejas; el modelo producido es único para cada geólogo y no se puede replicar, lo que hace que la auditoría por parte de personal externo sea una tarea difícil. Por otro lado, es inflexible, ya que modificar el modelo a medida que se dispone de nuevos datos lleva mucho tiempo, esto hace que el modelo no se actualice de forma regular.
Sin embargo, pese a las desventajas antes señaladas el resultado es un modelo confiable, al ser interpretado y evaluado de principio a fin por personal experto en la geología del depósito mineral.
Modelamiento implícito
Se define como un proceso en el que el modelo geológico se obtiene evaluando un conjunto de datos de entrada mediante una función matemática a través del espacio. Este método esta automatizado por lo que no requiere de la interacción manual como es el caso del modelado explicito. El objetivo sigue siendo el mismo; predecir la extensión espacial de las unidades geológicas a partir de los sondajes de exploración.
Una de las metodologías más prácticas para modelar implícitamente, es la de función de distancia con signo propuesta en el año 2003 por Osher y Fedkiw en el libro “Level Set Methods and Dynamic Implicit Surfaces”, la cual está basada en la interpolación de distancias obtenidas entre las ubicaciones de los datos, en nuestro caso a partir de los atributos geológicos obtenidos de sondajes.
La función de distancia por signo mide la separación que existe entre dos unidades geológicas distintas, donde se asignan distancias positivas y negativas a partir de una condición; estar dentro o fuera de una unidad geológica determinada.
Función de distancia con signo
La forma de proceder con esta metodología se explica a través de cuatro pasos:
Primero se debe codificar la variable categórica geológica de forma binaria, es decir, si pensamos en 2 unidades geológicas (A como principal y B como secundaria), A tomará el valor numérico de 1 y B tomará el valor numérico de 0. Ha de considerar que esta función solo es aplicable sobre una variable con 2 categorías, sin embargo, es extensible a múltiples categorías en su forma denominada “función de distancia con signo múltiple”, la cual explicare en otra oportunidad ya que por ahora solo nos convoca el entender la esencia del método implícito.
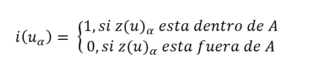
El segundo paso es calcular las distancias entre las unidades geológicas contra puestas. Si la muestra corresponde a la unidad A, la distancia tomara signo negativo, mientras que si es al revés, la distancia será positiva.
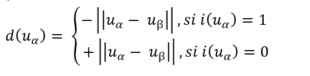
El tercer paso consiste en la interpolación de las distancias calculadas, lo tradicional es que se utilice una función de base radial (RBF) o kriging ordinario, sin embargo, es posible ocupar cualquier tipo de interpolador exacto, inclusive el inverso de la distancia. Los puntos o bloques donde la estimación resulte igual a cero (0), marcaran el contacto de ambas unidades geológicas.
Finalmente se codifican las distancias estimadas como:
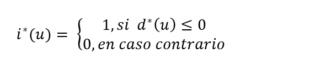
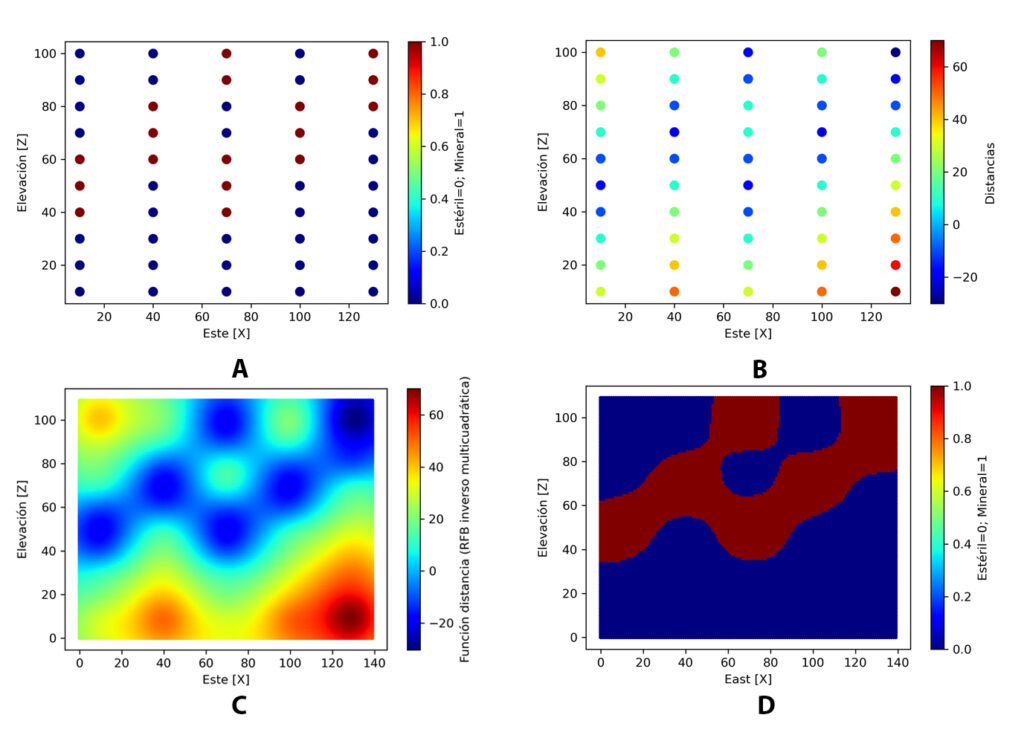
Ejemplo 2D para un caso binario
En (A) se presentan los compositos de mineral y estéril, en (B) se calculan las distancias, en (C) se realiza la interpolación con una función de base radial, en (D) se codifican las distancias estimadas en mineral y estéril.
Los interpoladores de función de base radial fueron introducidos por Hardy en 1971 en el artículo “Multiquadric equations of topography and other irregular surfaces”. Entre todas las técnicas de interpolación que existen, las RBF son útiles en ausencia de datos, y pueden ser una alternativa cuando los resultados obtenidos por kriging no son precisos debido al bajo número de observaciones o el incumpliendo de los supuestos requeridos por métodos geoestadísticos.
Los interpoladores RBF consisten en definir una función sf del tipo:
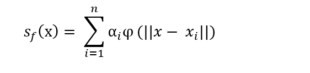
En nuestro caso ||·|| será la norma euclidiana en Rd, donde d es la dimensión del espacio. Los coeficientes α1, α2, . . ., αn se determinan resolviendo el sistema lineal que proviene de:
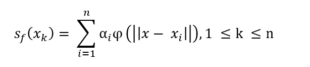
La elección de la función φ(r) en este ejemplo es multi cuadrática (φ(r) = √1+(€r)²), donde € es un parámetro de forma.
Ejemplo 2D para un caso de múltiples dominios
El modelado geológico de depósitos minerales involucra la interpretación de múltiples dominios. Sin embargo, el modelado geológico implícito descrito anteriormente (Funciones de distancia con signo), solo puede aplicarse para casos binarios. La función de distancia con múltiples dominios (ver ejemplo en la figura a continuación) es muy similar a la anterior, sin embargo agrega nuevas variables con distancias según el número de dominios existentes, y tiene una codificación final distinta. En esta oportunidad no detallare en este tema, sin embargo ejercicios a mano, ejemplos 2D, 3D de este y otros enfoques los pueden estudiar en: CURSO DE TÉCNICAS DE MODELAMIENTO GEOLÓGICO.
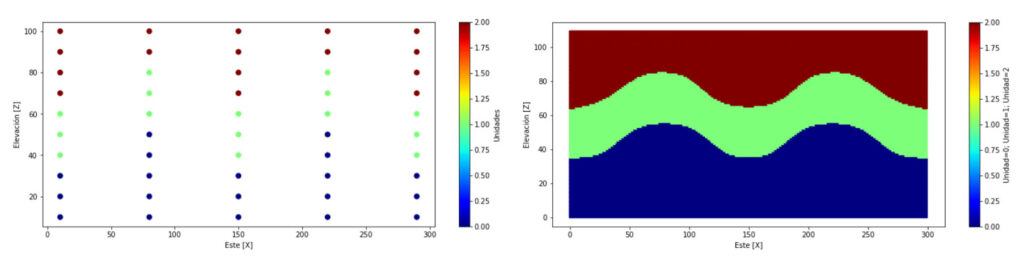
Conclusiones
El modelamiento implícito presenta una gran ventaja en cuestión de tiempo con respecto al modelado explicito, tiene la capacidad de generar múltiples unidades geológicas complejas en paralelo, también permite la reproducción del modelo únicamente con parámetros de entrada (auditable), sin embargo, este enfoque no reemplazará al geólogo modelador experto en el depósito mineral, es decir no se confía en una función matemática para la construcción de los pilares de la estimación y cuantificación de recursos minerales. Entonces, una mixtura de estos enfoques logra ser mucho más conveniente, pudiendo inicialmente partir con un modelo implícito, para luego ser chequeado y corregido manualmente por el geólogo experto de forma explícita.
Referencias
Cáceres, A., Emery, X., Aedo, L., & Gálvez, O. (2011). Stochastic geological modeling using implicit boundary simulation. In Proceedings of the 2nd International Seminar on Geology for the Mining Industry GEOMIN (p. 21).
Osher, S., & Fedkiw, R. (2003). Signed distance functions. In Level set methods and dynamic implicit surfaces (pp. 17-22). Springer, New York, NY.
Silva Maureira, D. A. (2015). Enhanced geologic modeling with data-driven training images for improved resources and recoverable reserves.
Vollgger, S. A., Cruden, A. R., & Cowan, J. E. (2013, August). 3D implicit geological modeling of a gold deposit from a structural geologist’s point of view. In 12th SGA Biennial Meeting-Mineral Deposit Research for a High-Tech World (pp. 1-4). SGA, Uppsala, Sweden.
Yardimci, A. G., & Basarir, H. (2015). A Contemporary Approach in Geotechnical Slope Stability Analysis: Lithological Implicit Modelling. In 24th International Mining Congress of Turkey (p. 710). The Chamber of Mining Engineers of Turkey.
