OPTIMIZACIÓN DE LOS LIMITES DE DISEÑO EN MINERÍA A CIELO ABIERTO
Tabla de contenidos
Breve reseña sobre la optimización de pit, y los métodos computarizados más emblemáticos.

Figura 1. Límites de la explotación minera a cielo abierto Chuquicamata, Chile
Optimización de pit
El procedimiento general de optimización de un rajo (pit), funciona en base a dos entradas: modelo de bloques valorizado y ángulos de talud por zonas del rajo, donde los taludes introducen restricciones en la precedencia de remoción de los bloques mismos.
El resultado de la optimización es una selección de bloques que representan el escenario de máxima ganancia respetando los ángulos de talud y bajo un cierto escenario económico. Las investigaciones para resolver el problema de optimización de pit utilizando un algoritmo de computadora comenzaron en la década de 1960, antes que eso el seleccionar la envolvente optima del rajo era un proceso manual.
El algoritmo de Lerchs-Grossmann (LG) fue publicado en 1965 y fue uno de los primeros métodos para producir la envolvente económica que define los límites del diseño minero. En la década de 1980, se implementó el primer paquete industrial con el algoritmo LG en Whittle Three-D.
El método LG se ha convertido en el estándar de la industria para la optimización de pit y también forma parte imprescindible del plan de estudios de ingeniería de minas.
El problema principal con el método LG es la cantidad significativa de tiempo que se requiere para determinar la envolvente económica optima, a medida que los modelos de bloques son de mayor tamaño.
Después de la publicación de LG, encontrar el pit óptimo ya no fue una tarea desafiante. En el ámbito académico, se ha centrado un esfuerzo significativo en la búsqueda de algoritmos de optimización, que sean más eficientes.
Se han entregado muchas alternativas prometedoras. En 1976, Picard demostró que el problema de optimización del pit se podía resolver con algoritmos de flujo máximo de manera más eficiente. En 1988, Goldberg y Tarjan desarrollaron un algoritmo de flujo máximo altamente eficiente llamado método Push-Relabel. En particular, en 2008, Hochbaum publicó un algoritmo de pseudoflujo, que demostró ser más eficiente que el LG y otros algoritmos de flujo máximo predominantes.
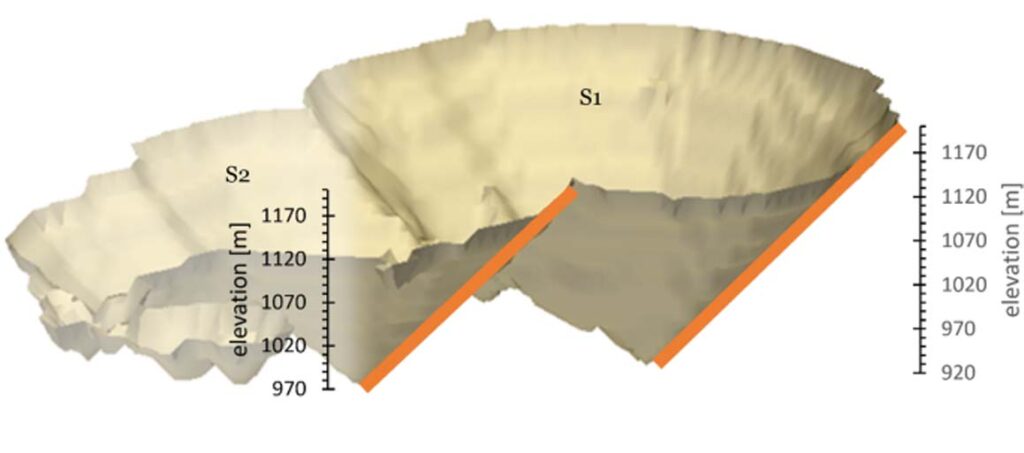
Figura 2. Ejemplo de una envolvente económica generado por la optimización
Antes de los algoritmos computarizados
Antes del desarrollo de métodos de optimización de pit computarizados, los ingenieros de mina debían utilizar métodos manuales de interpretación, lo cual básicamente consistía en dibujar en diferentes secciones transversales los límites de la explotación, a partir de las variables conocidas del depósito mineral y presentadas en el modelo de bloques. Claramente esta metodología presentaba ciertos problemas, de los cuales los más relevantes eran:
1. El basto tiempo que denotaba su elaboración.
2. La subjetividad, ya que distintos ingenieros presentaban distintas envolventes con los mismos datos.
3. El enfoque 2D en el que se desarrollaba la metodología, entendiéndose que realmente era un problema 3D.
Método del cono móvil flotante
Este método fue desarrollado en Kennecott Copper Corporation a principios de la década de 1960 y fue el primer intento computarizado de optimización de pit, que requirió un modelo de bloques tridimensional del depósito mineral.
La principal diferencia con el método manual es que el cono móvil flotante considera tres dimensiones (h= altura, w = ancho, l = largo), donde el modelo de bloques es analizado mediante la construcción de una forma cónica en dirección inversa y moviendo su vórtice de un bloque de mena a otro. La forma del cono es definida de manera tal que esté conforme con las restricciones de pendiente de talud de diseño del pit en las distintas áreas del depósito. El computador es utilizado en la generación de los conos 3D y en el cálculo del valor neto de cada cono, mediante la suma de los valores de todos los bloques de mena y estéril encerrados dentro del cono.
Finalmente, un límite 3D del pit es obtenido mediante la estructura global de todos los conos invertidos.
Este método requiere de un gran esfuerzo computacional, ya que debe analizarse de forma independiente cada uno de los bloques de mena, por lo que computacionalmente no es eficiente. Otra desventaja de este enfoque es que crea conos superpuestos y es incapaz de examinar todas las combinaciones de bloques adyacentes.
Método de Lerch & Grossman
En 1965 Lerchs y Grossmann publicaron un artículo que introdujo dos enfoques de modelado para resolver el problema de optimización a cielo abierto. Este método no se podía utilizar en la práctica hasta que Jeff Whittle de Whittle Programming Pty Ltd desarrolló un programa de optimización llamado Whittle Three-D a mediados de la década de 1980.
El algoritmo Lerch & Grossman (LG) mezcla la teoría de grafos, que es un enfoque heurístico, con un algoritmo de programación dinámica, que es una aplicación de una técnica de investigación de operaciones. El algoritmo genera un límite de tajo óptimo para un flujo de efectivo sin descontar, basado en un modelo de bloque económico de un cuerpo mineral y sus respectivos desechos circundantes. Como resultado entonces se obtiene una porción del modelo de bloques que garantiza el máximo beneficio económico.
LG toma en cuenta por una parte los taludes mineros requeridos, es decir opera bajo una restricción dada por la naturaleza geotécnica del macizo rocoso. Cada bloque en el modelo considerará la situación de sus bloques vecinos, es decir existirá una asociatividad económica entre bloques para determinar su extracción. Esta información se almacena como «arcos» entre los bloques («nodos»).
Dados los valores de los bloques (positivos y negativos) y los arcos de estructura, el método LG construye progresivamente una lista de bloques relacionados en forma de ramas de un árbol. Se buscan arcos de estructura, de manera tal que una rama de valor positivo que se encuentra por debajo de una rama de valor negativo se reestructure para que sea aceptable su extracción conjunta. Esto puede implicar combinar las dos ramas en una sola.
La verificación continúa hasta que no hay un arco de estructura que va de una rama positiva a una rama negativa. En este punto, los bloques en todas las ramas positivas tomadas en conjunto constituyen y definen el rajo óptimo.
En efecto, lo que ha hecho el algoritmo LG es encontrar el cierre máximo de un grafo dirigido ponderado; en este caso, los vértices representan los bloques en el modelo, los pesos representan la ganancia neta del bloque y los arcos representan las restricciones de minería (ángulo de talud).
Como tal, el algoritmo LG proporciona una solución matemáticamente óptima al problema de maximizar el valor del pit (considere que esto es para un valor de flujo de caja no descontado).
Cabe señalar que es una solución matemática y funciona solo con una lista de vértices y una lista de arcos. Si estos se presentan en una, dos o tres dimensiones y cuántos arcos por bloque se utilizan es irrelevante para la lógica del método, que es puramente matemática.
También tenga en cuenta que transcurrieron unos 20 años entre la publicación del método LG (1965, que también fue el año en que se computarizó el método del cono flotante) y la primera adopción comercial disponible del método LG (Whittle’s Three-D). Sume a eso que desde la publicación del método LG a la fecha van 58 años, y sigue vigente y aceptado en la industria.
Método Pseudoflow
En su artículo de 1965, Lerchs y Grossmann indicaron que el problema del pit final podría expresarse como un problema de flujo de red de cierre máximo, pero recomendaron su enfoque directo, posiblemente debido a las limitaciones de memoria de la computadora en ese momento. Por lo tanto, el algoritmo LG fue un método para resolver un caso especial de un problema de flujo de red. (Deutsch, et al, 2015).
En 1976, Picard “proporcionó una prueba matemática de que un problema de flujo de red de “cierre máximo” (de los cuales el problema de optimización de pit es uno) era reducible a un problema de flujo de red de “corte mínimo”, por lo tanto, solucionable por cualquier algoritmo de flujo máximo eficiente. Como consecuencia, se podrían usar sofisticados algoritmos de flujo de red en lugar del algoritmo LG, y se pueden calcular resultados idénticos en una fracción de tiempo”. (Deutsch, et al, 2015).
Uno de los primeros algoritmos eficientes de flujo máximo utilizados para resolver el problema de optimización de pit fue el algoritmo de “Push–relabel maximum flow algorithm” (Goldberg y Tarjan, 1988; King et al., 1992; Goldfarb y Chen, 1997).
“El estudio de Hochbaum y Chen (2000) mostró que el algoritmo push-relabel superó al algoritmo LG en casi todos los casos. Cuando el número de vértices es grande, superior a un millón, los algoritmos de flujo de red realizan órdenes de magnitud más rápido y calculan exactamente los mismos resultados”. (Deutsch, et al, 2015).
Ha continuado el desarrollo de algoritmos de flujo de red más eficientes. El algoritmo más eficiente aceptado actualmente de pseudoflujo fue desarrollado por la profesora Dorit Hochbaumn y sus colegas en la Universidad de California, Berkeley (Hochbaum, 2002, 2001; Hochbaum y Chen, 2000).
Los métodos de pseudoflujo dan nueva vida a la optimización de pit de LG. El aumento de la velocidad puede ser de 2 a 50 veces más rápido que con los métodos LG y, teóricamente, mucho más rápido para problemas más grandes (Muir, 2005).
En 2020 Sebastián Avalos y Julián Ortiz de la Universidad de Queens (Canadá), publicaron una guía para la optimización de pit con el método de Pseudoflujo en lenguaje Python, la cual puede ser utilizada como base para trabajos a nivel universitario en caso de no contar con los software comerciales que actualmente lo implementan.
