
FUNDAMENTOS
El Krigeado Ordinario, desde ahora KO, es un modelo matemático que data de los años 60, propuesto por el Dr. George Matheron (geo matemático Francés fundador de la geoestadística), que busca dar solución al problema de la estimación de leyes en bloques, a partir de datos que se encuentren dentro de una denominada zona de dependencia (homogeneidad).
El KO, básicamente trabaja encontrando la mejor estimación lineal posible de la ley de un bloque, considerando la información disponible tanto al interior como al exterior del bloque que se requiere estimar.
A continuación se puede observar la formula lineal del estimador [Z*(x)]:
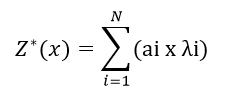
Donde:
- ai: Ley de la muestra conocida
- λi: Ponderador asociado a la muestra conocida
El estimador es insesgado y asegura minimizar la varianza de estimación. Esto último corresponde a una virtud del krigeado, dado que maximiza el provecho de la información, para obtener una estimación más precisa.
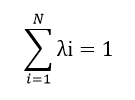
Es importante comentar que el KO, trabaja desconociendo el valor de la media de la variable regionalizada. Sin embargo su aplicación debe ser en dominios de carácter estacionario, conociendo momentos de segundo orden como el variograma γ (h) o la función de covarianza C(h).
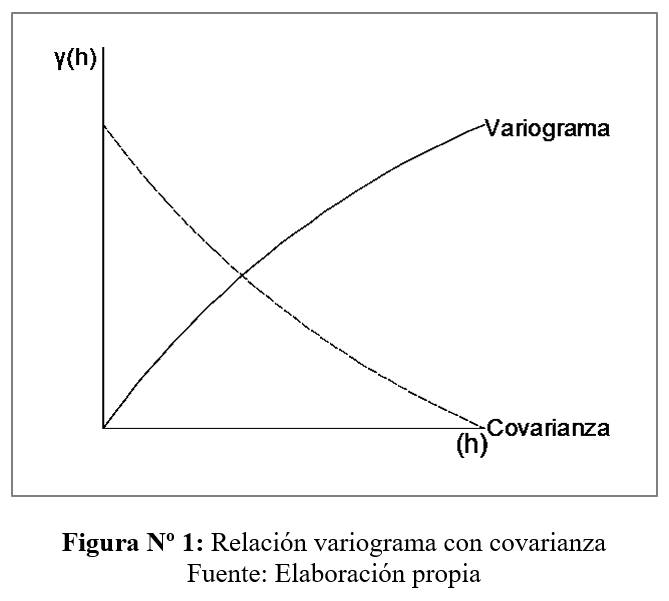
La relación queda establecida según la siguiente ecuación:
C(h) = C(0) - γ(h)
Donde:
- C(h): Covarianza
- C(0): Covarianza en el origen ó varianza σ²
- γ(h): Semivariograma
Las ponderaciones asignadas por este estimador a las muestras conocidas, se establecen a través de un sistema de ecuaciones normalmente expresadas con los valores del semivariograma:
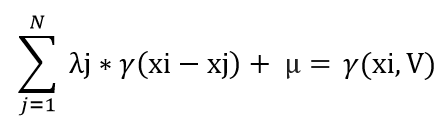
De este sistema, se observa que son estudiadas las redundancias entre los datos conocidos y las correlaciones entre datos conocidos y puntos a estimar.
La expresión “μ”, corresponde al multiplicador de Lagrange, que para fines de este documento, entenderemos como una acción necesaria para obtener la condición de insesgo.
La varianza de estimación del método, se obtiene a partir de la siguiente formula:
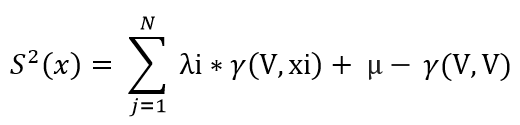
Donde:
- γ(V;xi): varianza de dispersión punto volumen
- γ(V;V): varianza de dispersión volumen volumen
- λi: Ponderación asignada a la muestra
- μ: Multiplicador de Lagrange
Entonces las ecuaciones del krigeado por bloques expresadas con el semivariograma, serán:
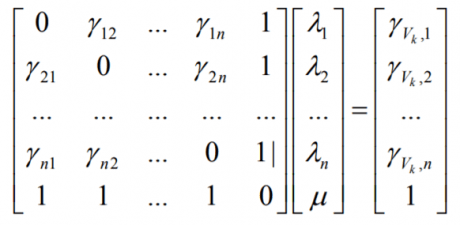
EJEMPLO
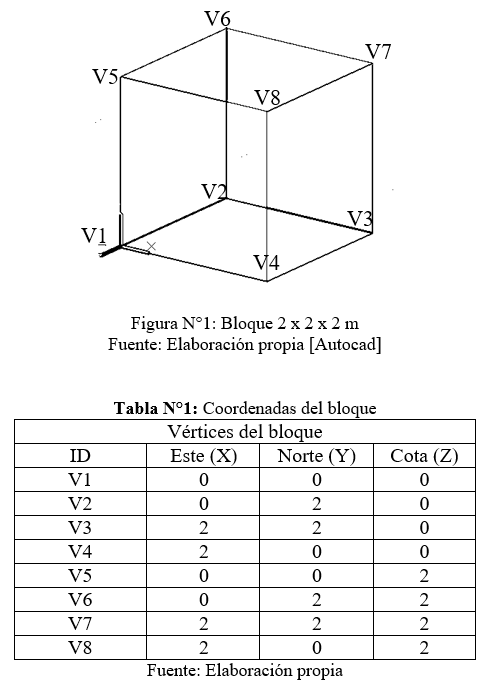
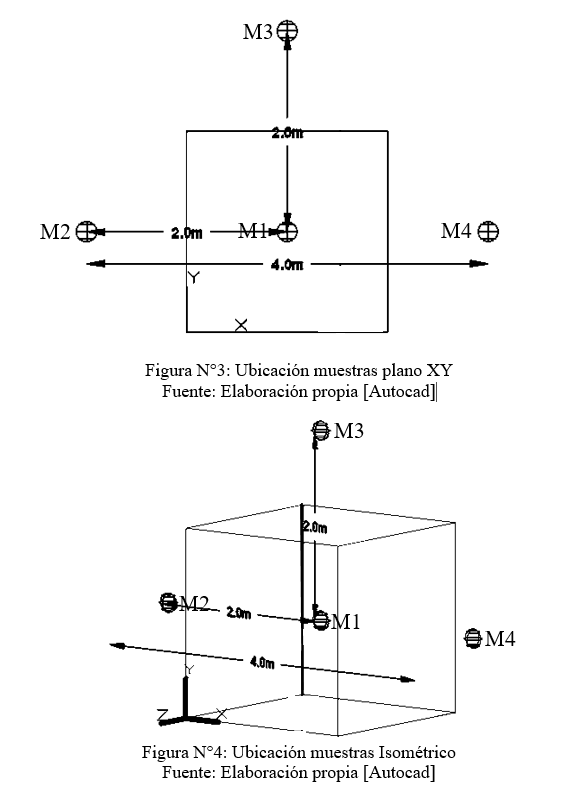
Se desea estimar la ley media [Z*(x)] de un bloque con dimensiones 2 x 2 x 2 (m), a partir de 4 muestras (puntos) conocidos y visualizados en este documento como esferas.
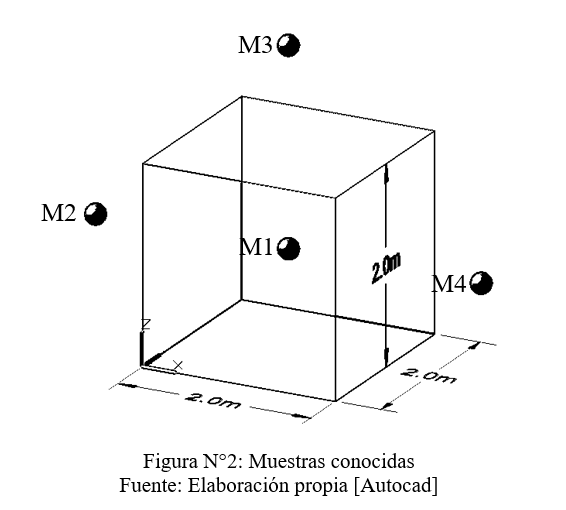
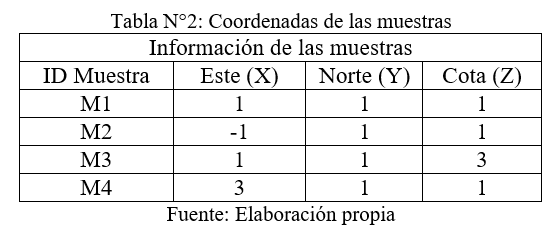
El modelo estructural, en este caso es de comportamiento isótropo y se conoce como γ(h) = 1.2 (h/10), de lo cual se deduce una meseta de valor 1.2 y un alcance máximo de 10 metros (zona de influencia).
Las distancias entre muestras, las cuales son necesarias para determinar las varianzas de dispersión entre muestras [γ(xi-xj)], quedan dispuestas según la tabla N° 3.
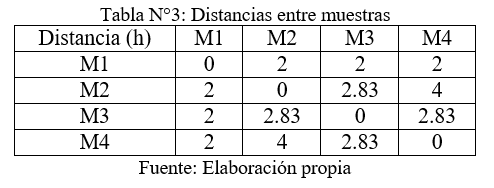
Luego las varianzas de dispersión entre las muestras, utilizando el modelo matemático esférico, quedan representadas en la tabla N° 4.
γ(h) =Co + C*[1.5*(h/a)]-[0.5*(h/a)³]
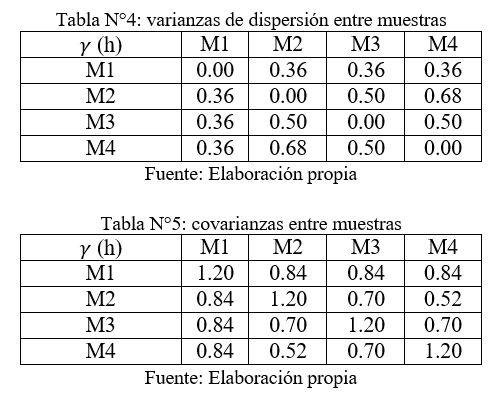
Para calcular las varianzas de dispersión entre las muestras y el bloque [γ(V;xi)], es que se debe discretizar el volumen en una serie de nodos (puntos).
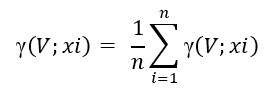
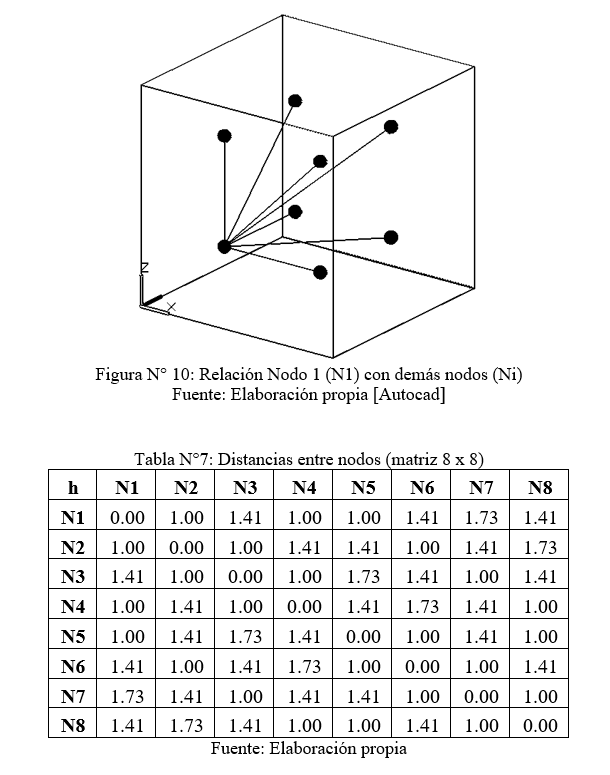
En este caso y al tratarse de un ejemplo manual, es que se discretiza el volumen total en ocho nodos. Se procede dividiendo en ocho sub-bloques y posteriormente trazando el nodo en el centro de cada sub-bloque.
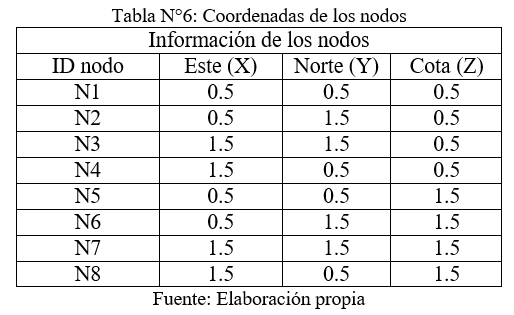
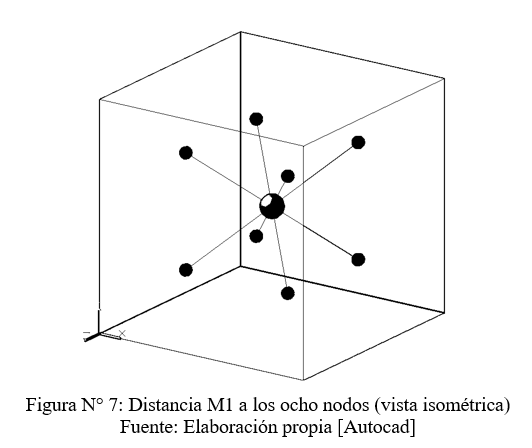
Conociendo las coordenadas de los nodos, se puede calcular [γ(V;M1)], [γ(V;M2)], [γ(V;M3)] y [γ(V;M4)]
Para el caso de la muestra N° 1 (M1), ubicada en el privilegiado lugar del centro del bloque, la varianza de dispersión punto volumen, queda definida como:
γ(V;M1)= γ(M1;N1) + γ(M1;N2) + γ(M1;N3) + γ(M1;N4) + γ(M1;N5) + γ(M1;N6) + γ(M1;N7) + γ(M1;N8)/ 8
γ(V;M1)= γ(0.866)*8/8
γ(V;M1)= γ(0.866)
γ(V;M1)= 0.16
Luego [γ(V;M2)] queda definida como:
γ(V;M2)= γ(M2;N1) + γ(M2;N2) + γ(M2;N3) + γ(M2;N4) + γ(M2;N5) + γ(M2;N6) + γ(M2;N7) + γ(M2;N8)/ 8
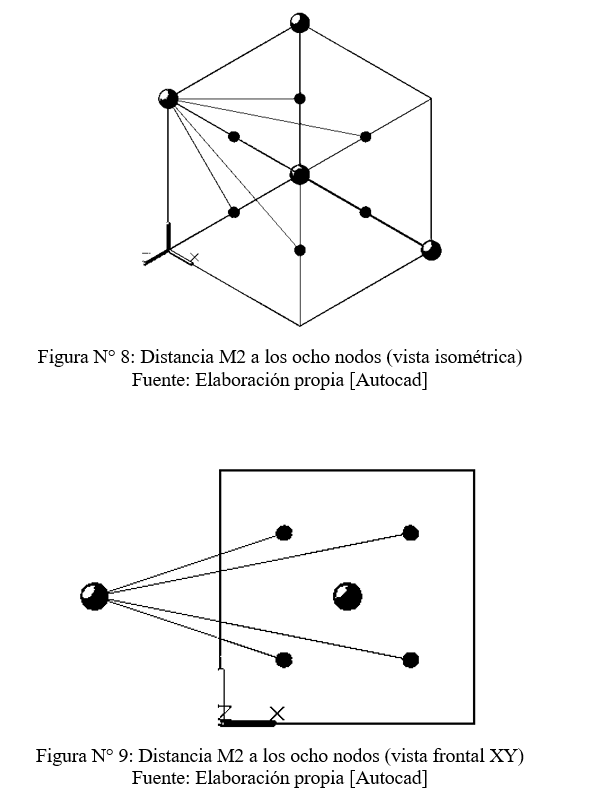
Reemplazando las distancias [M2; Ni] de la formula anterior [γ(V;M2)]:
γ(V;M2)= γ(1.6583) + γ(1.6583) + γ(2.5981) + γ(2.5981) + γ(1.6583) + γ(1.6583) + γ(2.5981) + γ(2.5981)/8
γ(V;M2)= [γ(1.6583)]*4 + ["γ(2.5981)]*4/8
γ(V;M2)= [(0.3*4) + (0.46*4)]/8
γ(V;M2)= 0.38
Por geometría, sabemos que [γ(V;M2)] = [γ(V;M3)] = [γ(V;M4)], por lo que sus dispersiones punto volumen, serán identicas.
Ordenando el sistema de ecuaciones del krigeado ordinario en función al semivariograma:
0.00*λ1+0.36*λ2+0.36*λ3+0.36*λ4+μ=0.16
0.36*λ1+0.00*λ2+0.50*λ3+0.68*λ4+μ=0.38
0.36*λ1+0.50*λ2+0.00*λ3+0.50*λ4+μ=0.38
0.36*λ1+0.68*λ2+0.50*λ3+0.00*λ4+μ=0.38
λ1+λ2+λ3+λ4=1
Ordenando el sistema de ecuaciones del krigeado ordinario en función a la covarianza:
1.20*λ1+0.84*λ2+0.84*λ3+0.84*λ4+μ=1.04
0.84*λ1+1.20*λ2+0.70*λ3+0.52*λ4+μ=0.82
0.84*λ1+0.70*λ2+1.20*λ3+0.70*λ4+μ=0.82
0.84*λ1+0.52*λ2+0.70*λ3+1.20*λ4+μ=0.82
λ1+λ2+λ3+λ4=1
Sea el sistema de γ (h) o C (h) que se resuelva, los ponderadores obtenidos [λi] serán los mismos. En este caso se utilizan el semivariograma.
- λ1 = 0.59
- λ2 = 0.16
- λ3 = 0.10
- λ4 = 0.16
- μ = 0.01
Haciendo uso del estimador lineal insesgado del krigeado ordinario para el bloque [V], se obtiene:
Z*(x)ko = [(0.59*M1) + (0.16*M2) + (0.10*M3) + (0.16*M4)]
La varianza de estimación del krigeado ordinario, queda expresada como:
S^2 (x)ko= [(0.59*0.16) + (0.16*0.38) + (0.10*0.38) + (0.16*0.38)] + 0.01 - γ(V,V)
Con esto, nos vemos en la necesidad de estimar la varianza de dispersión volumen volumen [γ(V,V)] para obtener la varianza de estimación del KO.
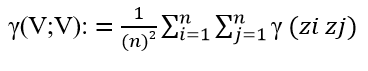
Para la obtención de γ[V;V], se requiere conocer la relación de varianzas de todos los nodos que discretizan el volumen.
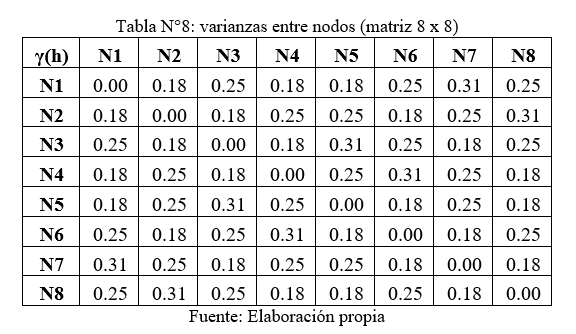
Luego empleando la fórmula de varianza de dispersión volumen volumen:
γ(V;V): =1/(8)^2 [(0)8+(0.18)24+(0.25)24+(0.31)8]
γ(V;V): =1/64[4.32+6+2.48]
γ(V;V): =0.20
S^2 (x)ko= [(0.59*0.16) + (0.16*0.38) + (0.10*0.38) + (0.16*0.38)] + 0.01 - 0.20
S^2 (x)ko= 0.064
Finalmente se puede obtener [Z*(x)] y [S²(x)] para cualquier valor de [Mi].



Debe estar conectado para enviar un comentario.