
En el presente articulo hablare acerca del beneficio de utilizar un algoritmo de aprendizaje automático, la sencillez de su implementación conociendo un poco de programación y los principales hitos en su puesta en marcha para con un caso sintético 7D.
Dominios de estimación:
Los dominios de estimación son el equivalente geológico a las zonas de comportamiento estacionario y se definen como un volumen de roca con controles de mineralización que resultan en distribuciones aproximadamente homogéneas. La definición y el modelado de estos dominios es un paso de suma importancia en la estimación de recursos minerales, dado que la correcta partición del depósito mineral en poblaciones homogéneas, disminuirá el sesgo condicional característico de la estimación geoestadística. Los dominios de estimación no son intrínsecos, deben ser creados y tener sentido espacial como geológico (Coombes, 2008).
Definición automática de dominios:
Resulta útil el implementar algoritmos de aprendizaje automático en la definición de dominios de estimación, primero por ser una tarea subjetiva, diferentes criterios o interpretaciones, resultaran en múltiples escenarios desde la misma información de entrada. Luego el tiempo que denota un proceso manual a uno automatizado, marca la diferencia de forma notoria. Por último y en caso de no confiar en nuevas técnicas, el tomarse como método alternativo o comparativo sin duda aporta un beneficio al trabajo.
Dentro de los algoritmos de aprendizaje automático no supervisados, los cuales se caracterizan por no poseer etiqueta, no entrenarse previamente, si no que trabajar directamente sobre los datos, está el popular k-medias (k-means).
K-medias pertenece al grupo de algoritmos de agrupamiento automático (clustering) y es empleado en niveles exploratorios de análisis de datos. Su popularidad se debe a que es multidimensional y posee una excelente escalabilidad.
Básicamente funciona agrupando los datos por una medida de similitud y requiere ser inicializado asignándole el número de grupos (k=1,2, 3, n). El algoritmo agrupa datos tratando de separar observaciones en n grupos de igual varianza, minimizando un criterio conocido como la inercia.
K-medias funciona siguiendo los hitos de:
- Inicialización: se elige la localización de los centroides de los k grupos aleatoriamente.
- Asignación: se asigna cada dato al centroide más cercano.
- Actualización: se actualiza la posición del centroide a la media aritmética de las posiciones de los datos asignados al grupo.
Los pasos 2 y 3 se siguen iterativamente hasta que no haya más cambios (mínima inercia).
En la siguiente animación inicializada con 3 grupos, se puede ver el funcionamiento de k-medias con 15 iteraciones hasta alcanzar la mínima inercia.
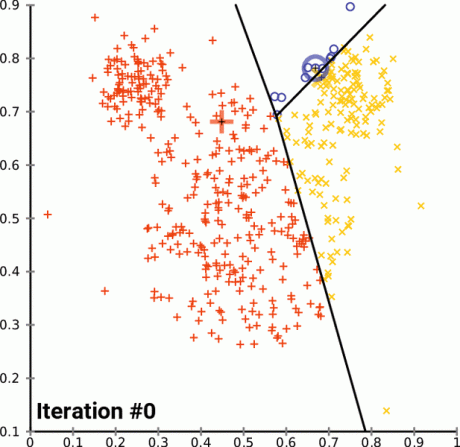
Limitaciones:
Una limitación bastante importante en la definición de dominios de estimación con este método, es que solo trabaja sobre variables numéricas. Entendamos que también tendremos variables categóricas, por lo cual para seguir con este enfoque y el uso de k-medias, tendremos que convertir desde categórica a numérica del tipo entera, pero con mucho cuidado, conociendo muy bien las relaciones de cada atributo geológico.
Caso sintético:
A partir de un caso, tratare de explicar brevemente cuales son los hitos que acompañan a la implementación del algoritmo k-medias, ya que se debe tener claro que este ultimo no realiza de forma individual todo el trabajo, si no que hay procesos complementarios que preparan la información y que por supuesto también se pueden automatizar.
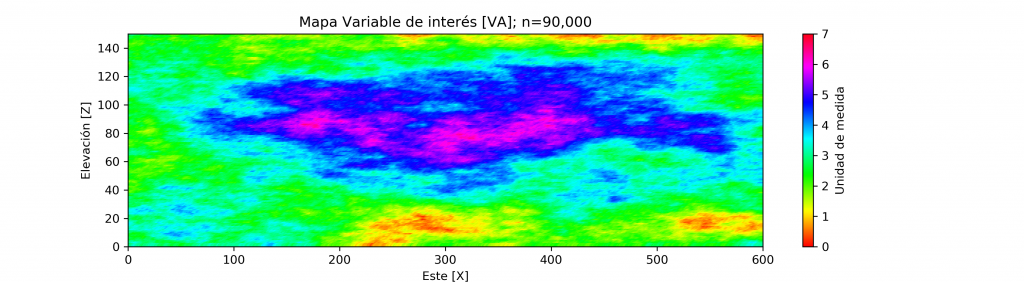
El caso sintético creado con uso de simulación geoestadística, corresponde a un escenario (perfil XZ) de 90,000 puntos, el cual en su atributo de interés principal (VA) que es una variable continua, refleja un comportamiento regionalizado anisotrópico con dirección principal en el eje horizontal (EW). La escala de la variable de interés oscila entre 0 a 7 (no se define una unidad de medida).
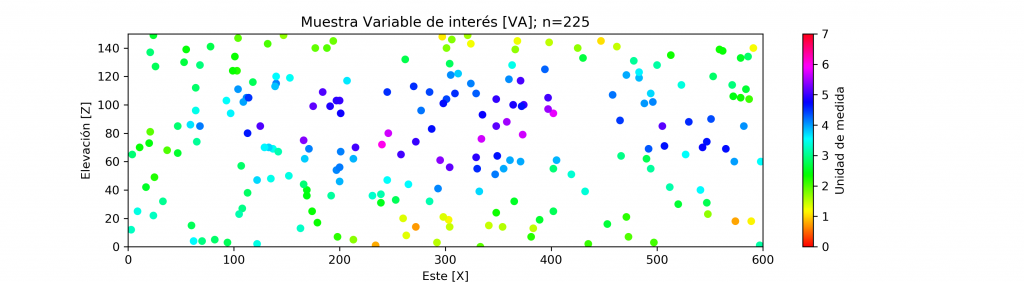
Desde dicho escenario es que se extrae una muestra de forma aleatoria equivalente al 0.25% de la población (n=225). Luego la variable principal (VA) es acompañada con 6 variables numéricas complementarias (VB, VC, …, VG), formando un conjunto de 7 atributos con 1,575 datos en total.
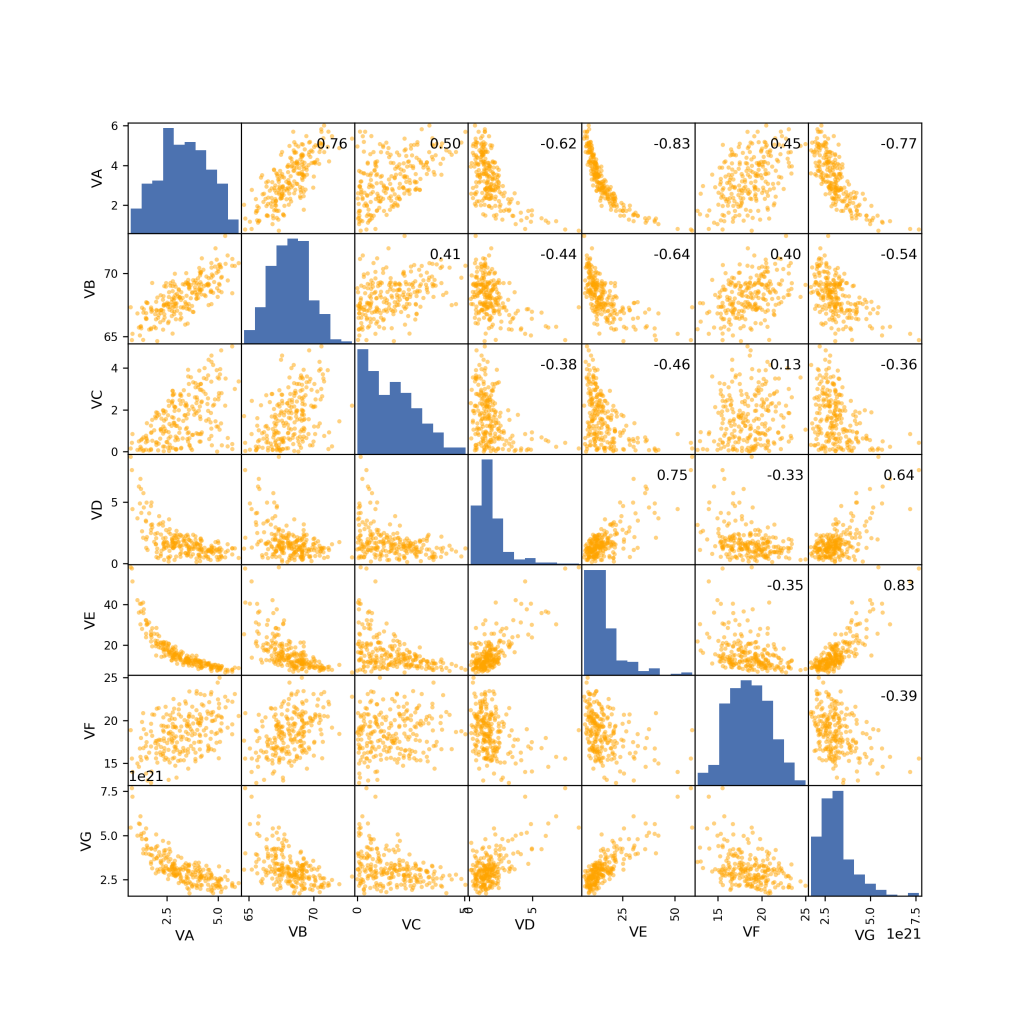
La dimensionalidad siempre ha sido un tema importante previo el uso de algoritmos de aprendizaje automático. Primero porque entre más atributos, más cálculos y tiempo de procesamiento. Mas importante aún, si no se manejan bien los atributos, unos podrían dominar al algoritmo y pasar a llevar a otros no dándole el peso necesario.
En este caso para ejemplificar lo anterior, entendiendo que solo tenemos 7 dimensiones, pero no sabemos si es que todas ellas aportan o no en el resultado. Se implementa previo al agrupamiento con k-medias, un análisis de componentes principales (ACP), el cual buscara dejar solo aquellas componentes incorrelacionados y que representen la mayor varianza del conjunto.
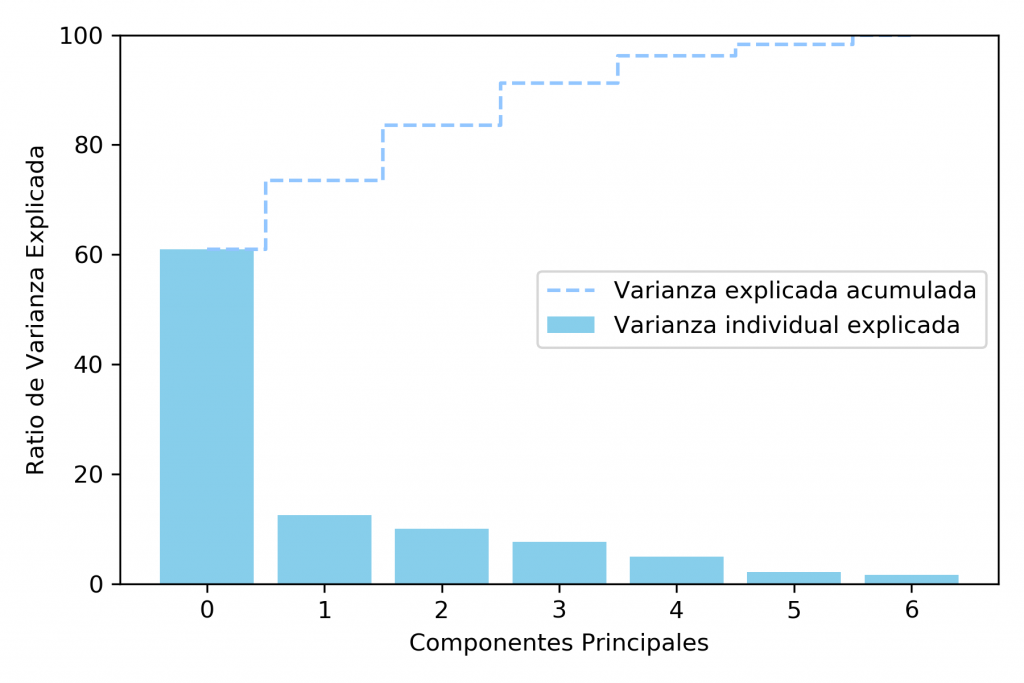
Del gráfico se observa que con 4 componentes (desde 0 al 3) se tiene explicada el 92% de la varianza, por lo que en este caso reduciremos la dimensionalidad desde 7 a 4. Importante señalar que en caso de que no se busque una extracción de características con PCA, el eliminar ciertas dimensiones de forma directa, es una alternativa.
Es importante señalar que las variables previo al agrupamiento con k-medias, deben poseer la misma escala y no mezclar unidades de medida distintas. Por ejemplo, una concentración de cobre a nivel porcentual como atributo 1, con concentraciones en partes por millón de oro como atributo 2, no deben ser utilizadas si es que antes no se estandarizan.
Ya con el nuevo conjunto de datos y una vez reducida la dimensionalidad, es que pasamos a escoger el numero de grupos k. Para ello es que utilizamos una heurística de nombre método del codo, la cual compara un numero de grupos en función de su inercia. Importante saber que también existen otro métodos para seleccionar el optimo k, como son la silueta y el índice Calinski Harabasz.
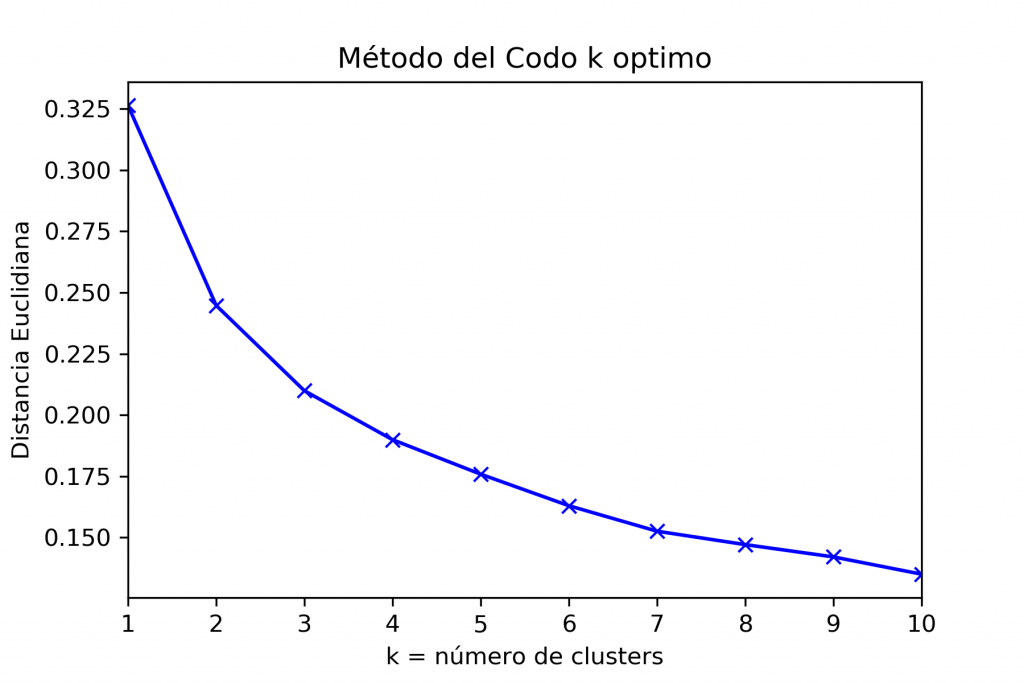
En el eje horizontal se encuentra el numero de grupos realizando pruebas desde 1 a 10 grupos. En el eje vertical se encuentra la inercia. El numero optimo de “k”, es cuando se genera un cambio de pendiente, una inflexión en la curva, siendo en este caso cuando k=3.
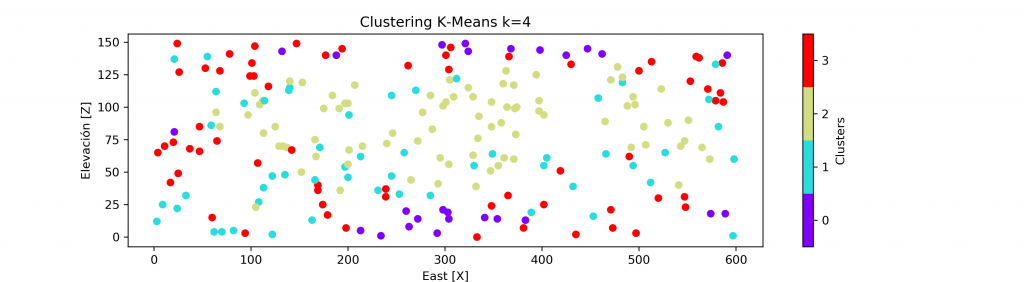
A continuación, se presenta el resultado del agrupamiento para cuando k = 2,3,4.
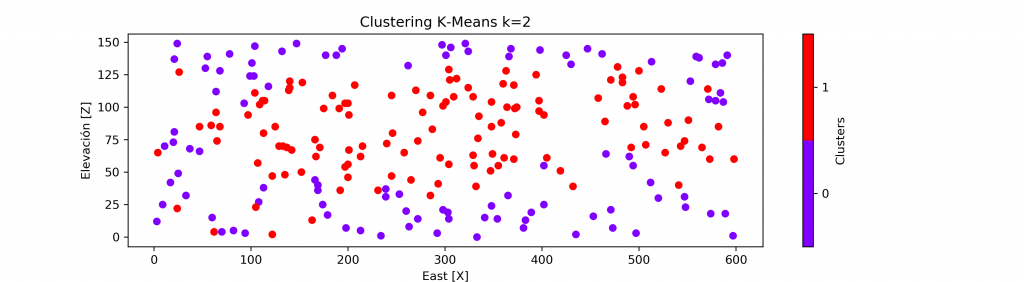
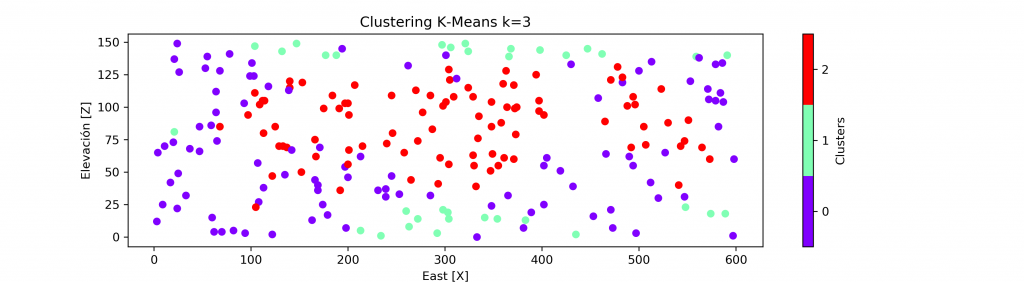
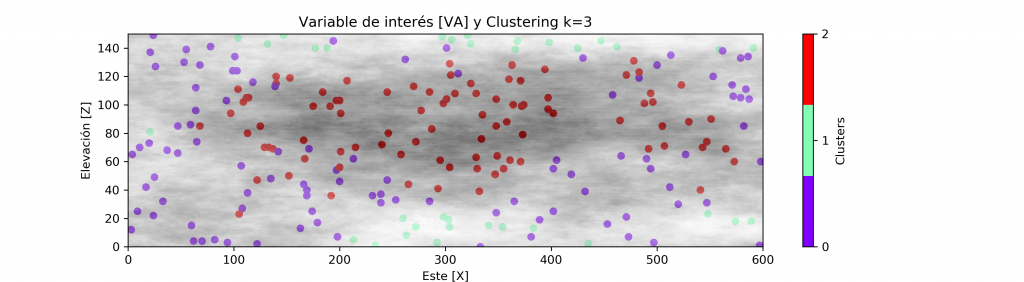
Dejando un background en escala de grises para el atributo principal (VA), podemos ver una correcta agrupación en base al cambio de los valores. Existiendo un grupo para valores bajos, medios y altos.
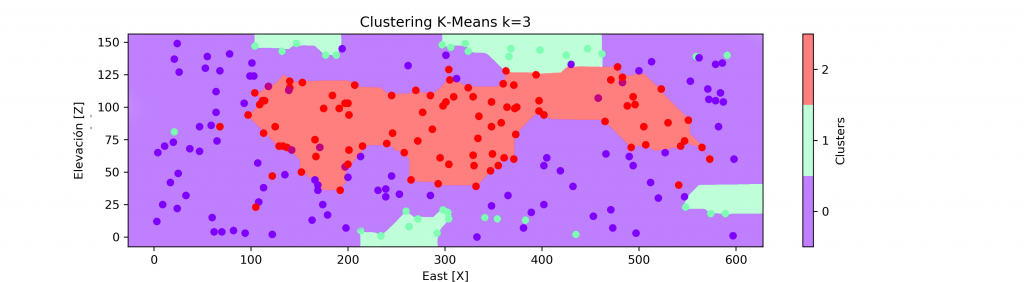
La definición de los dominios de estimación, se presenta como:
Conclusiones y trabajos pendientes:
De forma evidente el coeficiente de variación de la variable principal (VA) post generación de 3 grupos, se reduce considerablemente siendo esta una buena medida de representatividad de la media y homogeneidad por grupo.
- CV[VA] Cluster 0: 0.194832
- CV[VA] Cluster 1: 0.255291
- CV[VA] Cluster 2: 0.156118
Para validar el agrupamiento se recomienda además:
- Generar un análisis de deriva por cluster (estudiar el comportamiento de la media y varianza).
- Realizar un semivariograma omnidireccional por cluster (descartar presencia de tendencia).
El algoritmo parece funcionar bastante bien, su implementación con la biblioteca de Scikit Learn en código Python fue sencilla, rápida, solo queda seguir validando su utilidad, realizar estudios con datos reales e incluir ahora el Este (X), Norte (Y) y Elevación (Z), que dan un carácter espacial al agrupamiento.
Tambien evaluar otras alternativas para combatir el problema de la mixtura en el tipo de datos (numérico – categórico), como puede ser el pasar ahora de numérico a categórico y utilizar k-modas, que justamente es una variación de k-medias para datos categóricos, y ver cuanta información es la que se sacrifica. O bien ir mas allá y probar nuevos métodos como k-prototypes, que trabaja directamente con estos dos tipos de datos.


Debe estar conectado para enviar un comentario.