REDES NEURONALES VS KRIGING

CONTEXTO: ESTIMACIÓN DE RECURSOS MINERALES
(HERNÁNDEZ H. - 12 de Julio 2023)
Tabla de contenidos
En este breve post mostrare los resultados de implementar redes neuronales en el proceso de estimación de una variable numérica continua, en un escenario simulado y muestreado 2d. Específicamente dos tipos de redes; El Perceptrón Multi-Capa (1) y una Red Neuronal de Función de Base Radial (2). Luego seran comparados los resultados con Kriging Ordinario.
¿Por qué estimar fuera del enfoque geoestadístico?
Básicamente para evitar dos cosas: el supuesto de estacionariedad de la variable de interés (1) y el modelado espacial a través del muchas veces subjetivo variograma (2).
¿Por qué Redes Neuronales?
La creciente popularidad del aprendizaje de máquinas en diversos campos se atribuye principalmente a los avances en la capacidad de cómputo (Samson, 2019), a la disponibilidad de grandes volúmenes de datos que permiten entrenar modelos complejos, y a su capacidad para integrarse fácilmente con otras disciplinas aplicadas. En los últimos veinte años, los métodos basados en aprendizaje de máquinas han ganado popularidad en la investigación de estimación de recursos. Varios estudios (Samanta, Banopadhyay y Ganduli, 2006; Chatterjee, 2010; Tahmasebi y Hezarkhani, 2010; Zhang, 2017) han destacado que los métodos basados en el aprendizaje de máquinas han surgido como modelos de predicción y alternativas importantes a la geoestadística. El algoritmo de aprendizaje de máquinas más utilizado en la estimación de recursos minerales son las redes neuronales artificiales (Dumakor y Arya, 2021). Estas redes son modelos computacionales que ofrecen una simplificación abstracta del cerebro humano. Conceptualmente, imitan el funcionamiento de las redes neuronales biológicas para reconocer relaciones en un conjunto de datos y predecir valores de salida para datos de entrada dados. Están compuestas por capas de nodos interconectados que representan neuronas artificiales (Shanmuganathan, 2016).
¿Se han usado Redes Neuronales para la Estimación Recursos?
El primer caso registrado del uso de una red neuronal artificial en la estimación de recursos minerales se documenta en el trabajo de Wu y Zhou (1993). En su estudio emplearon un perceptrón multicapa como tipo de red neuronal para estimar la ley de un depósito de cobre, utilizando las coordenadas espaciales como variables de entrada. Al-Alawi y Tawo (1998) también utilizaron una red neuronal entrenada con las coordenadas espaciales, pero se centraron en estimar el grosor de las longitudes mineralizadas en un depósito de bauxita, junto con el contenido de alúmina y sílice. Samanta et al. (2002) emplearon un sistema de inferencia neuro-borroso adaptativo, que es un tipo de red neuronal, para estimar la ley mineral en un depósito de oro y compararon los resultados con el método de kriging. Concluyeron que el algoritmo de aprendizaje de máquinas presentaba mejores resultados que la geoestadística en su caso de aplicación. Dutta et al. (2010) compararon diversos estimadores geoestadísticos con redes del tipo perceptrón multicapa y SVM. Concluyeron que las diferencias en las métricas de error eran marginales. Jafrasteh et al. (2018) sugieren que, además de las coordenadas espaciales, incluir características del macizo rocoso que tengan algún control sobre la variable objetivo ayudaría a reducir el error de estimación. Por ejemplo, Kaplan y Topal (2020) estimaron la ley mineral en un depósito de oro utilizando información de las coordenadas espaciales en 3D, la litología y la alteración hidrotermal. Obtuvieron resultados prometedores que indican que las redes neuronales podrían ser una alternativa viable frente a los métodos geoestadísticos.
Perceptrón Multicapa y Red de Función de Base Radial
Explicar el Perceptrón Multicapa tomaría mucho texto, se puede estudiar de forma estándar en cualquier libro relacionado con aprendizaje de máquinas. Solo diré que es un tipo de red neuronal de propagación hacia adelante con una arquitectura basada en 1 capa de entrada, «1,2,3…n» capas ocultas y 1 capa de salida. Luego la Red Neuronal de Función de Base Radial, viene hacer una simplificación de la anterior, ya que solo ocupa 1 capa oculta y la función de activación de sus neuronas en dicha capa son funciones de base radial. Ambas redes se entrenan con el algoritmo de retro propagación (ajuste de pesos óptimos).
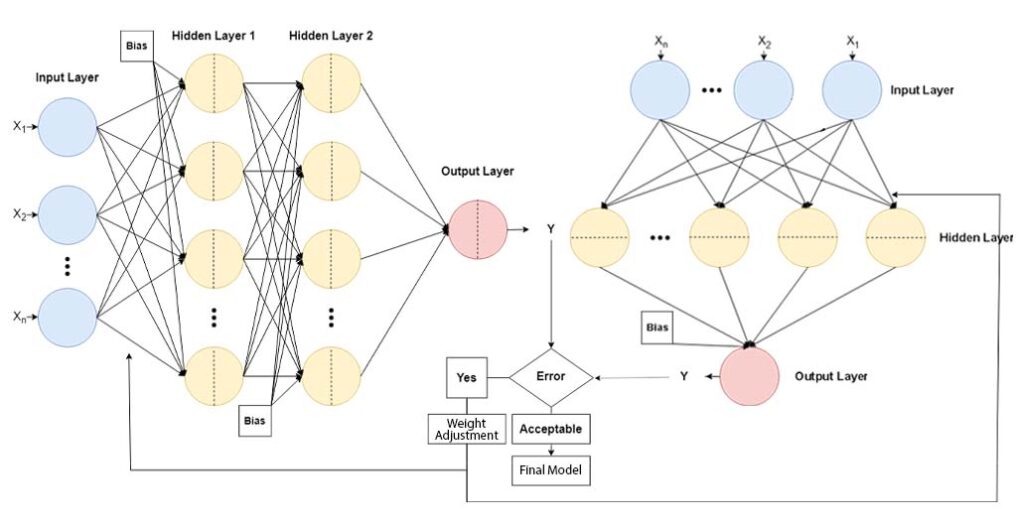
Perceptrón Multi-Capa (izquierda), Red Neuronal de Función de Base Radial (derecha).
Sondajes 2d
Para el primer ejemplo se ocupa un escenario 2d simulado geoestadísticamente (variograma omnidireccional de 500 metros de alcance), se corrige la media y la desviación estándar y se dispone a sacar una muestra del 5%.
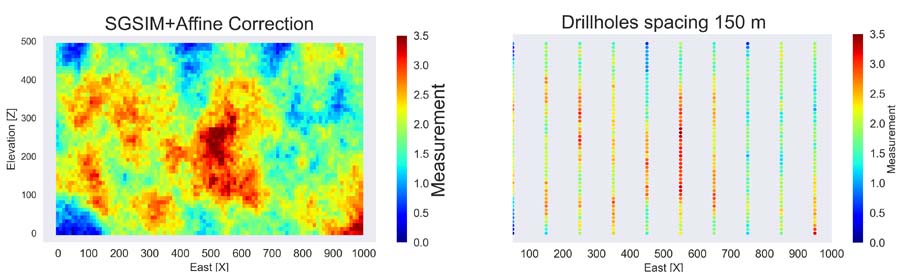
Resultados
El Kriging se ocupa bajo un escenario perfecto de conocimiento sobre la variabilidad espacial (un sueño), es decir se ocupa con el mismo modelo variografico con el que se crearon los datos simulados. Esto último ya lo colocaría inmediatamente sobre cualquier otro enfoque de estimación. En este ejemplo solo optamos a ver que tanto se acercan las redes neuronales al Kriging.
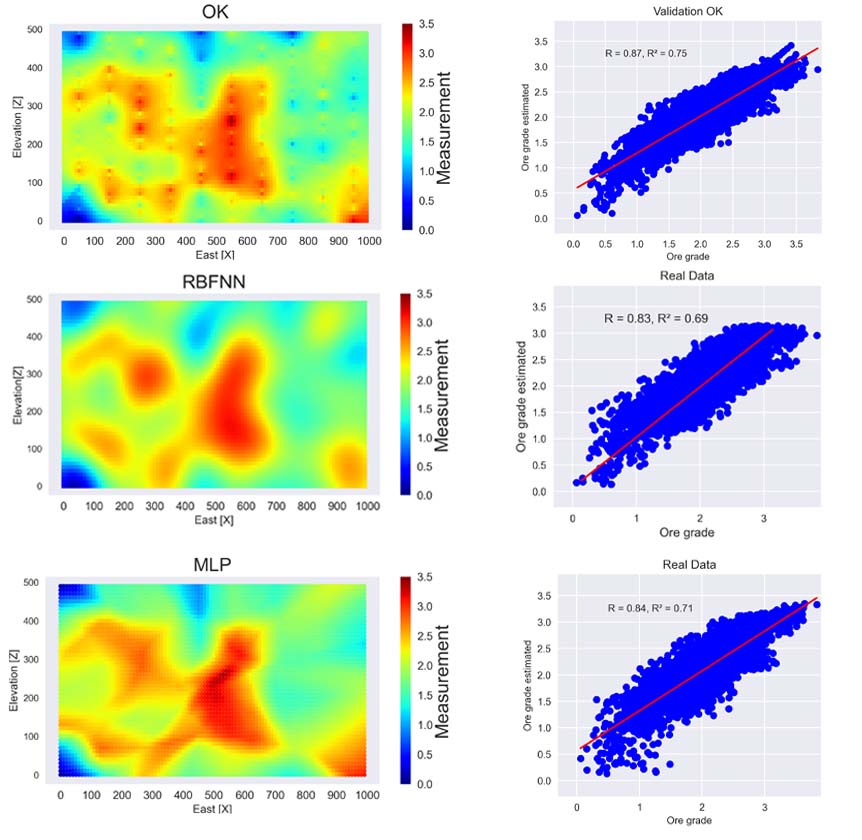
En cuanto a la arquitectura de las redes, muy por encima diré que el perceptrón multicapa utilizo las coordenadas espaciales de la variable de interés en la capa de entrada (X,Z), 3 capas ocultas con 56 neuronas cada una (todas activadas con funciones ReLU) y una capa de salida sin ninguna función de activación. Como función de optimización se ocupo ADAM y se necesito tunear la red para encontrar resultados llamativos para el ejemplo, es decir hiper-parámetros que llegaran a métricas de validación similares al Kriging. En cuanto a la red de función de base radial, esta fue levemente mas baja en cuanto a las métricas (RMSE, R, R^2), pero notablemente más eficiente en cuestiones de tiempo (realmente rápida).
¿Influencia de la densidad de muestreo?
Este es un tema que amerita un poco más de profundidad, es decir tanto la densidad del muestreo como la disposición espacial de la muestra (comparar los métodos con distintos escenarios). De todas formas únicamente modificando el tamaño de la muestra desde 1% a 3% de la «realidad» simulada, es que los resultados mantuvieron lo esperado en base al ejemplo anterior del 5%.
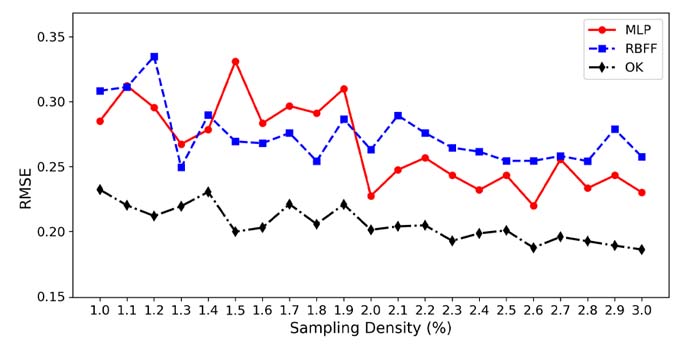
Conclusiones
En cuestión de validación las redes neuronales anduvieron realmente cercanas al mejor Kriging posible, además no necesitaron de un variograma si no que únicamente de las coordenadas espaciales para entrenarse y estimar valores en lugares no muestreados. Es un tema que si bien se ha estudiado bastante en los últimos años, aun requiere más pruebas en distintos tipos de variables y ambientes. Más importante aún de la aceptación de la industria.
Referencia web:
Hernández, H. (12 de julio de 2023). Redes Neuronales vs Kriging. Nube Minera. https://nubeminera.cl/redes-neuronales-kriging
